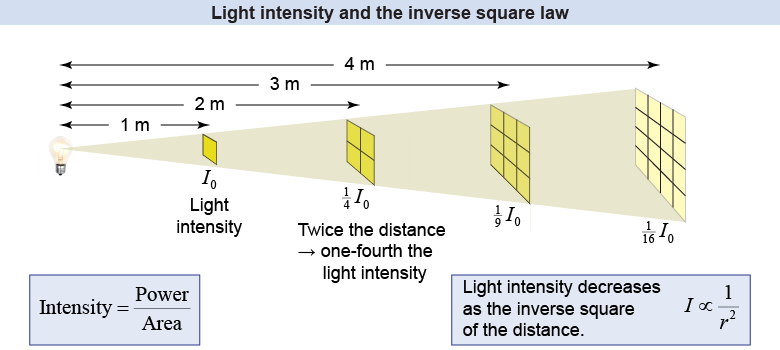
|
The brightness of light is described by intensity I, which has units of watts per square meter (W/m2). Thus intensity is a measure of the power per unit area, as shown in equation (20.1). The Sun, a bright light source, has an intensity around 500 W/m2. The light of a flashlight spot on the floor in a darkened room might be 1 W/m2. 
|
| (20.1) | | | I | = | light intensity (W/m2) | | P | = | power (W) | | A | = | area (m2) |
| Light intensity
|
|
|
As you move farther from a light source, the intensity of light decreases as the inverse square of the distance. Going twice as far decreases the intensity by 22 = 4. This is not a law of physics but a result of geometry. Consider the light from a point source that emits a total power P equally in all directions. At any distance r, the power is spread out over a sphere of area 4πr2. The intensity of the light is I = P/(4πr2). A relationship in which a quantity decreases as 1/r2 is called an inverse square law. The intensity of light from a point source obeys an inverse square law.
|
|
Luminous intensity is a physical quantity related to intensity, but it is defined in a way that factors in the response of the human eye to visible light. The unit of luminous intensity is the candela (Cd), which is approximately the amount of visual light produced by a typical candle. Luminous intensity is one of the seven fundamental physical quantities of science.
|
|
The energy output of the Sun is called the solar luminosity L, which has a value of 3.8×1026 W. The Earth is 1.5×1011 m away from the Sun. At Earth’s orbit the intensity of sunlight is equal to the Sun’s luminosity divided by the area of a sphere the size of Earth’s orbit. This works out to 1,365 W m−2 at the top of Earth’s atmosphere.
|
|
The inverse square law appears in other aspects of physics as well as light. As you learned on page 214, the gravitational force follows an inverse square law. In Chapter 18, you learned that the electric force (Coulomb’s law) is also an inverse square law.
|
