|
We now have two equations that together make up a mathematical model of motion that includes position, velocity, acceleration, and time. Equation (4.2) describes velocity and equation (4.3) describes position. 
|
|
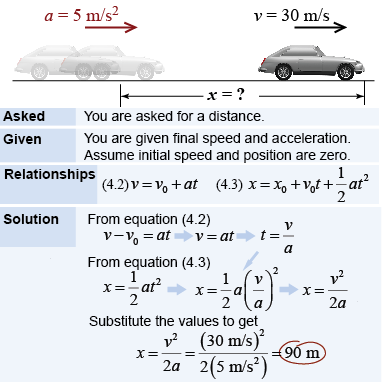Some problems require both equations. For example, consider a car that starts from rest with a constant acceleration of 5 m/s2. How far does the car go before it reaches a speed of 30 m/s (67 mph)? This problem asks for a distance but it gives you speed and acceleration. There are two unknown values: time and position. Therefore, to solve the problem you need both equations. - Equation (4.2) allows you to solve for the time in terms of the known final velocity and acceleration.
- Equation (4.3) gives you the position.
|
A car starts at rest at the top of a ramp. What is the acceleration if the car goes 1.4 m down the ramp in 1.6 s? - You are given position, time, and an initial velocity of zero. You only need equation (4.3) since there is only one unknown variable.
- Solve the equation for acceleration to find that a = 1.09 m/s2.
|
A car starts from rest at the top of a ramp that creates an acceleration of 2.1 m/s2. How much time does it take the car to travel 1 m? - You only need equation (4.3) since there is only one unknown variable.
- Solve the equation for acceleration and substitute values to find that t = 0.98 s.
|
