|
The general condition for static equilibrium has two parts, both of which must be satisfied: - The sum of forces must be zero in all directions (ΣF = 0).
- The sum of torques must be zero around any choice of center (Στ = 0).
The force equilibrium equation (8.1) can result in up to three equations, one for each coordinate direction. The torque equilibrium equation (8.3) adds at least one additional equation for each different choice of the center of rotation. 
|
|
|
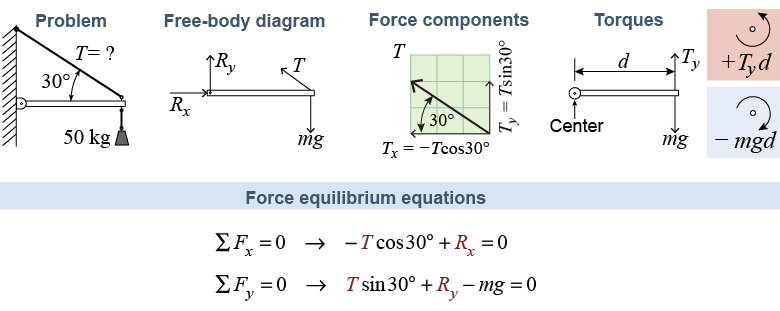
We can now solve the problem of the mass hanging from the beam. The two force equilibrium equations in x and y do not provide a solution. If we choose the center, however, to be the point where the beam attaches to the wall, then the two reaction forces (Rx, Ry) contribute zero torque since their line of action passes through the center. The same is true of the x-component of the tension Tx.
|
|
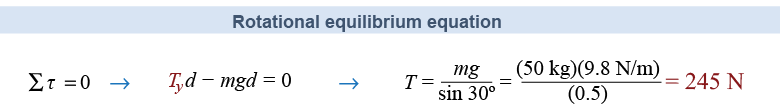
The two vertical forces create opposite torques. To be in rotational equilibrium, these torques must sum to zero. The resulting equation has only a single unknown value and can be solved directly for the tension T. Note that the problem is easiest to solve when the center is chosen to eliminate the torque from the unknown reaction forces Rx and Ry.
 |
Now that we know T, it is possible to solve for reaction forces Rx and Ry. Notice that Rx must point to the right to cancel the component of tension that acts toward the left. Therefore, What about Ry? It is not immediately easy to tell whether Ry points up or down or is zero. By solving the force equilibrium equation for the y-direction, we see that Ry equals zero. 
|
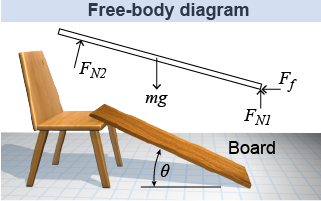Any type of force may exert a torque. Torques can be created by friction and also by normal forces and reaction forces. Normal forces act perpendicular to surfaces of contact. Friction forces act parallel to surfaces of contact. The example of a board resting on a chair and the floor shows both kinds of forces.
|
