|
In a static problem nothing moves, either in linear motion or rotation. Therefore, the net force must be zero. This condition is called equilibrium. Any object that remains at rest must be in equilibrium because, if there were any net force, then the object would accelerate and start moving. Equation (5.2) is the condition for equilibrium of forces. 
|
| (5.2) | | | F1, F2, F3, ... | = | force (N) |
| Equilibrium
|
|
This is a vector equation! That means that equation (5.2) holds separately for each direction relevant to the situation. - The total force in the x-direction must be zero.
- The total force in the y-direction must be zero.
- The total force in the z-direction must be zero.
 |
Equilibrium technically includes motion with constant velocity. Nonetheless, we usually apply equilibrium analysis to things at rest, or things we wish to stay at rest—such as buildings and structures. 
|
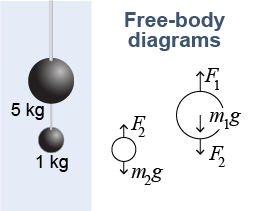Equilibrium problems often involve finding one or more unknown forces using the fact that the net force is zero. A free-body diagram is essential for keeping track of the directions and positions of forces. In the diagram on the right two iron balls are hung from rods. The free-body diagrams include the weight of each ball and the forces from the rods.
|
- Draw a free-body diagram including forces from ropes, attached supports, weight, and normal forces.
- Assign positive and negative directions.
- Use the equilibrium equation by setting the net force to zero independently for each direction. Each direction equation can be solved for one unknown force.
- If there are still unknown forces then you may need more information.
|
|
In many problems there may be a symmetry that causes some forces to be equal. In the example below, the forces from each rope must be equal because the acrobat is in the center, in a symmetrical position. That means that these forces can be assigned the same variable name F instead of separate names such as F1 and F2. The name is the same because the forces are known to be equal and therefore have the same value.
|
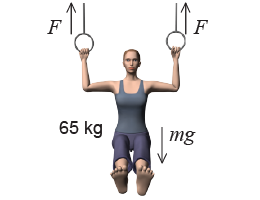A 65 kg acrobat is suspended motionless between two rings as shown at right. What is the tension force in the rope holding up one of the rings if the acrobat is centered between them? | Asked: | tension force F | | Given: | mass = 65 kg “at rest” | | Relationships: | Fw = mg; net force = 0. | | Solution: | 2F − mg = 0
| → F | = | ½mg | | = | (0.5)(65 kg)(9.8 N/kg) = 320 N | |
|
If, while moving at 9 m/s, a box experiences a friction force of 40 N, how much force do you need to apply to the box for it to be in equilibrium? - 0 N
- 20 N
- 40 N
- 80 N
 |
The correct answer is c, 40 N. When an object is in equilibrium, there is no net force. This means that you must cancel out the 40 N friction force by applying a 40 N force of your own. 
|
