|
If you know an object is moving with constant velocity v, can you predict the position of the object at any later time t? How? How do the equations we have developed so far lead to a model of constant-speed motion? 
|
|
The answer is to solve the velocity equation for the displacement Δx, then break Δx into the initial position xi and final position xf. The result is equation (3.5), which is really just a restatement of equation (3.3).
 |
In the next chapter we will introduce better notation for modeling velocity and distance as a function of time. Were we to use that notation here, the position x is a function of time: where x0 is the initial position at time t = 0. 
|
| (3.5) | | | xf | = | position at time t (m) | | xi | = | initial position at time t = 0 (m) | | v | = | velocity (m/s) | | t | = | time (s) |
| Position
constant velocity |
|
|
The position, time, and velocity in equation (3.5) are instantaneous values. This equation allows you to calculate the instantaneous position at any time when given the initial position and (constant) velocity.
|
A train leaves a station located 300 km from the start of a track. How far is the train from the start of the track if it travels for 8 hr at 100 km/hr? | Asked: | final position xf of the train | | Given: | v = 100 km/hr; xi = 300 km; t = 8 hr | | Relationships: | xf = xi + vt | | Solution: | The units are km/hr and hours, which are consistent: x = 300 km + (100 km/hr)(8 hr) = 1,100 km | | Answer: | 1,100 km |
|
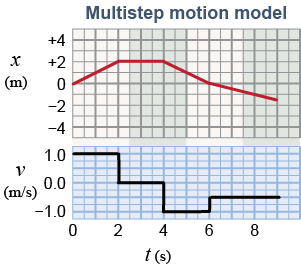You might think the limitation to constant velocity makes equation (3.5) useless in the real world. Nonetheless, complex motion can be accurately modeled by breaking up the time into intervals. The velocity is recalculated for each interval and is only considered constant during that interval. The final position for one interval becomes the initial position for the next interval. Many computer models use this approach, as do robots and self-navigating vehicles.
|
