| | Essential questions | | How do we predict an object’s position at a later time? | |
|
Graphs and equations are invaluable methods for describing the motion of an object. Position versus time and velocity versus time graphs can describe where an object is located, how fast it is going, and in which direction it is headed. Equation models allow us to predict a future value, such as position, from given information, such as velocity and starting point. Most equation models have parameters, such as initial position and velocity, which are adjusted to fit a specific situation or problem. 
|
Part 1: Matching the motion of an ErgoBot
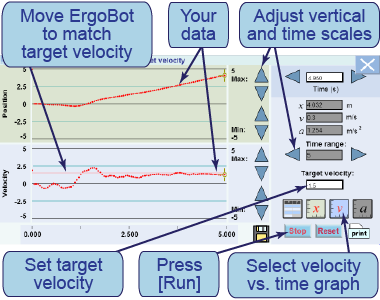In this activity, you will adjust the motion of an ErgoBot until its velocity graph matches with a target graph. - Set up the ErgoBot in freewheel mode and place it on the track.
- Select the velocity graph and enter a target velocity.
- Move the ErgoBot with your hand so that its motion matches the graph.
- How does the velocity graph for a high positive velocity differ from that for a lower velocity?
- How does the velocity graph for a negative velocity differ from that for a positive velocity?
- How does the position graph for a negative velocity differ from that for a positive velocity?
- Describe a situation for which the x vs. t graph and the v vs. t graph are both flat (zero-slope) horizontal lines.
|
In this interactive simulation, you will adjust the motion of the ErgoBot until a velocity vs. time graph of its motion matches that of a target graph.
|
Part 2: The constant-velocity model for position vs. time
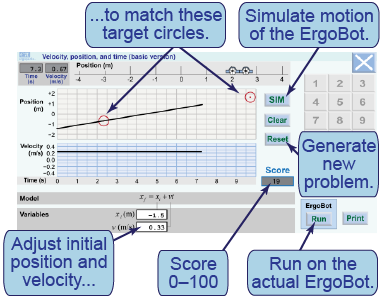This interactive, graphical model shows position and velocity versus time graphs for the motion of a “virtual” ErgoBot. Red circles on the position versus time graph are “targets.” Your goal is to adjust the initial parameters, xi and v, so that the line hits both targets. - [SIM] starts the simulation. [Stop] stops it without changing values. [Clear] resets all variables to zero. [Reset] resets all variables and sets new targets.
- Enter values in the white boxes. Gray boxes are calculated and cannot be edited. The top score of 100 is achieved by crossing the center of each target circle.
- Use the print button to print out a copy of your solution and score.
- Describe the meaning of xi and v in this model for the motion of the ErgoBot.
- What velocity will move an object from +50 m to −50 m in 20 s?
- Find a solution yourself, then press [Clear] and have your partner find a solution. How well do your two solutions agree? Is one solution better than the other?
|
In this interactive simulation, you will adjust the initial position xi and velocity v of the ErgoBot so that a position vs. time graph of its motion matches graphical targets.
|
Part 3: A more complex model
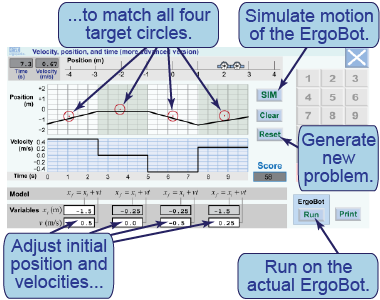
- The second interactive model contains four constant-speed segments.
- Your goal is to adjust the values of xi and v for all sections to hit the four targets.
- Enter values in the white boxes. The top score of 100 is achieved by hitting the center of each target.
- Simulate your model to see how it runs on the graphs of its motion.
- [Run] your model on the ErgoBot itself.
- In this model for the motion of the ErgoBot, there are four values of xi. Where do the three values of xi in the gray boxes come from?
- Describe how this model could be generalized to recreate any motion in one dimension.
|
In this interactive simulation, you will adjust the initial position xi and four different velocities v—for each of four time periods—of the ErgoBot so that a position vs. time graph of its motion matches graphical targets. Watch as you simulate the motion of the ErgoBot. Then run the same commands on the ErgoBot itself. Watch it go!
| | | |
| |
|
