| | Essential questions | | How do we quantitatively describe movements in space? | |
|
Within the next decade self-driving cars could make the leap from science fiction to dealer showrooms to people’s driveways. How does a self-driving vehicle represent movements? In this investigation we look at one- and two-dimensional displacement vectors and how they are added to create motion paths. 
|
Part 1: Displacements in one dimension
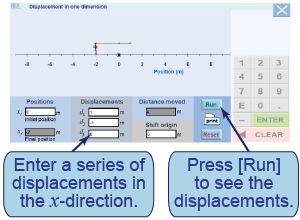The interactive simulation allows you to add multiple displacements in one dimension. You may also shift the origin. Use the simulation to solve the following problems. - A man moves 6 m east, stops, turns around, and moves 2 m west. What is his final position? How far did he travel?
- A woman starts at position −10 m and has three successive displacements of −5 m each. What is her final position?
- What displacement moves an object from an initial position of +25 m to a final position of −10 m?
- A robot starts at the origin. Use three different displacements to move the robot to a final position of +8 m, where the second displacement must be negative.
|
|
In this interactive element, you create a series of individual displacements and then run the simulation to create the total displacement. This simulation is entirely in one dimension.
|
Part 2: Displacements in two dimensions
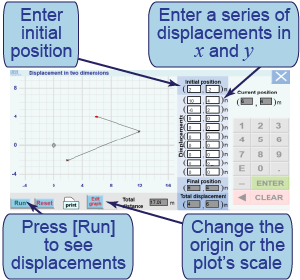The interactive simulation allows you to add multiple displacements in two dimensions. You may also reset the origin of the display. Use the simulation to solve the following problems. - What two perpendicular displacements will move an object from the origin to a position of (4, 3) m?
- What is the final position of a robot that starts from (0, 0) m and makes displacements of (4, 4) m, (3, 3) m, and (−4, −2) m?
- Create a path of four displacements of equal distance that move from a position of (1, 1) m to a position of (2, 2) m. Note that there are many possible solutions.
- A student starts at the origin and ends up at a position 500 m north of the origin. She knows she walked 250 m straight west, but then she was blindfolded and led to the final position. Assume she walked a straight path for the hidden leg of the trip. What is the displacement vector of her movement?
- What sequence of two displacements moves an object from (5, 5) m to (−5, −5) m while traveling a distance of exactly 20 m? How does this distance compare to the single displacement that connects the same starting and ending point?
- Create a series of eight successive displacements that would program a robot to move in an octagonal path that is as close as you can get to approximating a circle. The robot should return to its starting point after the eighth displacement. What total distance does the robot move? Calculate the radius of the circle that has this distance as its circumference.
|
|
In this interactive element, you create a series of individual displacements and then run the simulation to create the total displacement. This simulation is in two dimensions, x and y.
|
| |
|
