 A builder of musical chimes wishes to divide a 1 m length of pipe into four segments that have the following relationships between their lengths. Not wishing to have any waste, the builder knows it is possible to make three cuts that divide the pipe into exactly the four segments needed. - The longest pipe is twice the length of the shortest pipe.
- The second longest pipe is 4/5 the length of the longest pipe
- The third longest pipe is 2/3 the length of the longest pipe.
Calculate the lengths of each of the pipes.
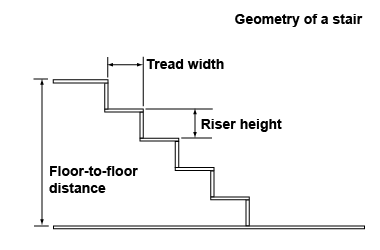
- The building code is a set of rules for how to design and build houses that are safe, strong, and comfortable. The rule for designing stairs is that twice the rise plus the run equals 25 in. The rise is the vertical distance between steps and the run is the tread width. A second rule is that the treads and risers must be the same for every step. The carpenter measures the height between floors and designs a stair that meets the rule by calculating a riser height and tread width that satisfies the rule while making all the risers equal and all the treads equal.
- Derive an equation that relates the riser height and tread width.
- Derive an equation that relates the distance between floors, the number of stairs, and the riser height.
- Suppose the distance between floors is 118 in. Use your equation to come up with two different stair designs that meet the rule but have riser heights no more than 9 in and tread widths no less than 9 in.
| | - Given that x1 + x2 = 4 m and that x1x2 = 4 m2 what are the possible values for x1 and x2?
 You are given two algebraic equations: y = 5x and 6y = x + 2. Solve for x and y.
- A skier leaves the lodge traveling at a constant speed of 12 m/s. Thirty minutes later, another skier leaves the same lodge traveling along the same trail. At what speed must the second skier travel to catch up with the first skier in 90 min?
- Two cyclists are riding a trail that makes a 5.5 km loop. Both start at the same place at the same time. One cyclist rides at an average speed of 25 km/hr. The other cyclist rides ahead, maintaining an average speed of 29 km/hr. For how much time do the two cyclists ride before they meet up again?
- Two boats are sailing directly toward each other at different speeds. One moves at 20 m/s and the other at 32 m/s. The boats start 2,500 m apart. How much time does it take before the boats collide?
- A car leaves a city traveling at a constant speed of 85 km/hr on a straight road. A second car leaves exactly one hour later traveling in the same direction. At what speed must the second car travel to catch up with the first car 250 km away from the city?
- Two hikers leave from different places on the same trail. Sonyia hikes at a constant speed of 4 km/hr starting from Arcos canyon at 1:00 pm. Marguarite starts from Arroyo canyon at 3:00 pm and hikes at 5 km/hr. If the two hikers meet up in 8 hr, then how far apart along the trail are Arcos and Arroyo canyons?
- A swimmer travels at 0.8 m/s heading south across a small lake. At the same time, a second swimmer heads north from the opposite shore at a speed of 0.4 m/s. How wide is the lake if the two swimmers meet 12 min later?
|
