|
The most basic elements of music are pitch and rhythm. The pitch of a sound is how high or low we hear its frequency. Pitch corresponds closely to frequency, but pitch is also a matter of perception. The way you hear a pitch can be affected by the sounds you hear immediately preceding, along with, and just after a note. Rhythm is the repeating time pattern in a sound. Rhythm can be loud or soft: tap-tap-TAP-tap-tap-TAP-tap-tap-TAP. Rhythm can be made with sound and silence or with different pitches. 
|
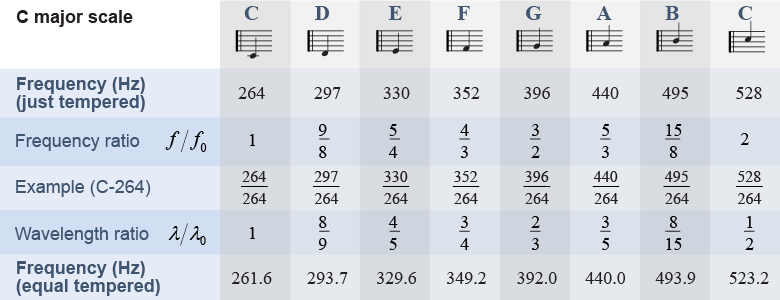
Although styles vary, all music is created from carefully chosen patterns of frequencies of sound called musical scales. Each frequency in a scale is called a note. The diagram below shows some of the notes on a piano along with their frequencies. There are eight primary notes in the Western musical scale, which correspond to the white keys on the piano. 
 |
The black keys on a piano come from the need to play music in different keys. The ratios in the diagram are based on the note C with a frequency of 264 Hz, or “C-264 Hz.” But a composer might want to begin the pattern on D-297 Hz instead of C; in other words, to set the music in the key of D major. The second note of the scale that begins on D has a frequency 9/8 higher than D, which is 334 Hz. This is pretty close to E-330 Hz. The third note, however, has a frequency of 5/4 × 297 Hz, or 371 Hz. This is between F-352 Hz and G-396 Hz and different enough to sound distinct from either F or G.
The solution is to put another note, F#, between F and G. If you go through the same process of starting the pattern of frequency ratios on successive notes other than C-264 Hz you find that five additional frequencies are needed for the “in-between” notes. These are the five black keys on the piano keyboard and they correspond to the notes C#, D#, F#, G#, and A#. 
|
|
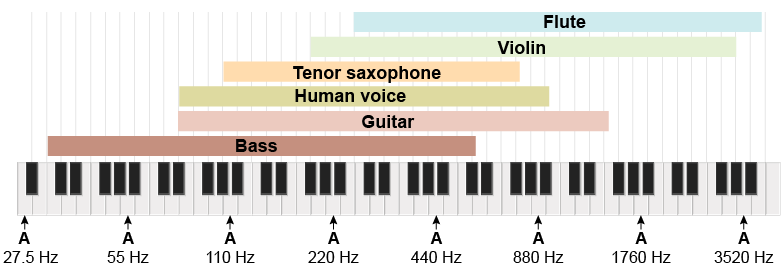
The range between a frequency and twice that frequency is called an octave. Notes that are an octave apart in frequency share the same name because they sound similar. An 88-key piano can play notes across a little more than seven full octaves, corresponding to a frequency range from A-27.5 Hz to high C-4186 Hz. 
|
|
The ratios of the scale were discovered in the sixth century BC by Pythagoras, whose mathematical analysis of sound forms the basis of Western music. Look at the frequencies in the top figure: All of the frequencies are spaced apart such that none make unpleasant beats with another and none of their harmonics make beats with the harmonics of other notes! Since the mid-18th century, however, Western music has adopted the equal tempered scale, containing frequencies that deviate slightly from these perfect ratios. 
 |
These ratios are known as the just tempered scale, and there is a single exception regarding overlap and beats where the third harmonic of one note is only 11 Hz away from the second harmonic of another note. Most modern instruments, including the piano, are tuned to a slightly different set of frequencies called the equal tempered scale. In the equal tempered scale the frequency intervals are logarithmic instead of multiplicative fractional ratios. The equal tempered scale has 12 frequency intervals and includes the black keys. The relationship between frequencies is that the nth note above the first note in the scale is 2n/12 times the frequency of the first note. In other words, each note (or semitone) is 21/12 = 1.0595 times higher in frequency than the preceding note. The advantage of the equal tempered scale, touted by the great composer Johann Sebastian Bach, is that the notes are equally in tune in any key. This is not true for the just tempered scale. 
|
| |
|

