Essential Physics

Binding energy


Why is binding energy important?	The energy E_b that must be supplied to separate a nucleus into its constituent protons and neutrons is called the binding energy. Different elements, and different isotopes, have different amounts of binding energy. For example, if eight protons and eight neutrons make two helium-4 nuclei, then the amount of binding energy is different compared to the same particles arranged as a single oxygen-16 nucleus. The difference in binding energy between isotopes provides the energy for nuclear reactions.
Nuclear mass deficiency	When free nucleons come together in a nucleus, the binding energy is released. That means the nucleus has less rest energy and therefore less mass than the separate particles it is made from. The difference in mass, called the mass deficiency, is exactly equal to the binding energy required to hold the nucleus together. Binding energy and the mass difference are related through Einstein’s mass–energy equivalence equation.
An example: nucleus of helium-4	As an example, consider the nucleus of helium-4, which has two protons and two neutrons. The mass of the individual protons and neutrons is 4.0319 amu. $Two protons: m_{2 p} = 2 \times (1.6726 \times 10^{- 27} kg) = 2 \times 1.0073 amu = 2.0146 amu$ $Two neutrons: m_{2 n} = 2 \times (1.6749 \times 10^{- 27} kg) = 2 \times 1.0087 amu = 2.0173 amu$ $Total mass of nucleons: m_{2 p} + m_{2 n} = 4.0319 amu$
	The mass of the helium-4 nucleus is 4.0015 amu. This is 0.0304 amu less than the sum of the masses of the individual protons and neutrons. The mass difference of 0.0304 amu is helium-4’s mass deficiency, equal to 28.32 MeV in energy units: $E_{b} = (0.0304 amu) \times (931.5 MeV/amu) = 28.32 MeV$
A more advanced binding energy calculation	The tabulated elemental masses are given as atomic masses rather than nuclear masses. When using the atomic mass in binding energy calculations, one has to take into account the mass of the electrons included in the atomic mass. This is done by using the mass of the hydrogen atom instead of the mass of the proton. The mass of the electrons cancels out and the result is the binding energy of the nucleus. Let’s go over the binding energy calculation for the boron-11 nucleus. Given: The atomic mass of boron-11 is m_B¹¹ = 11.00931 amu. The atomic number of boron is Z = 5. The mass of a neutron is m_n = 1.00869 amu. The atomic mass of hydrogen is m_H = 1.007825 amu. Relationships: 1 amu corresponds to 931.5 MeV. The atomic number of boron is 5. The number of neutrons is N = A − Z = 11 − 5 = 6. The mass deficiency is $\begin{array}{l} Δ m & = & Z m_{H} + N m_{n} - m_{B} \\ = & 5 (1.007825 amu) + 6 (1.00869 amu) - 11.0093 amu \\ = & 0.08194 amu \end{array}$ Solution: For the binding energy of the boron-11 nucleus E_b = (0.08194 amu)(931.5 MeV/amu) =76.329 MeV For the binding energy per nucleon of the boron-11 nucleus E_b/A = (76.329 / 11) MeV = 6.94 MeV
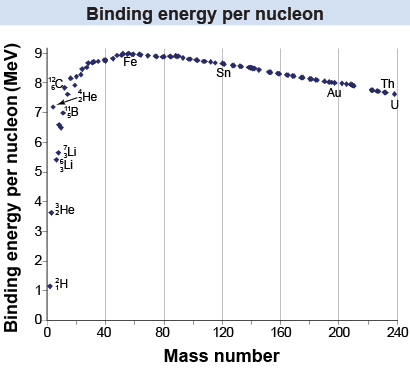Binding energy per nucleon	A useful quantity in nuclear physics is the binding energy per nucleon, or the binding energy E_b divided by the number of nucleons, A. For the example of helium-4, the binding energy per nucleon (E_b/A) is (28.3 MeV)/4 = 7.08 MeV. The binding energy per nucleon increases with atomic number up to element 56, which is iron (Fe). The binding energy per nucleon decreases slowly with atomic number for elements heavier than iron. The shape of the binding energy graph reflects a balance between the repulsion of the electric force (among the protons) and the attraction of the strong force (among the nucleons).
What does the binding energy graph mean?	The graph of binding energy per nucleon reflects the ultimate energy source of our universe. Stars release nuclear energy by combining light elements and moving from left to right, from hydrogen toward iron. Nuclear reactors release energy by splitting up heavy atoms and moving from right to left, from uranium toward iron.
Test your knowledge	Calculate the binding energy per nucleon for carbon-12. The atomic mass of carbon-12 is 12 amu.
	Let’s start by collecting all the information that we know. The atomic mass of carbon-12 is m_C¹² = 12 amu. The atomic number of carbon is Z = 6. Therefore, the number of neutrons is N = 6. The mass of a neutron is m_n = 1.00869 amu. The atomic mass of hydrogen is m_H = 1.007825 amu. Now we calculate the mass deficiency (Δm) for the carbon-12 nucleus: $\begin{array}{l} Δ m & = & 6 m_{H} + 6 m_{n} - m_{C^{12}} \\ = & 6 (1.007825 amu) + 6 (1.00869 amu) - 12 amu \\ = & 0.0990811 amu \end{array}$ Since there are 931.5 MeV per amu, the total amount of binding energy associated with a nucleus of carbon-12 is (0.0998011 amu) × (931.5 MeV/amu) = 92.3 MeV The binding energy of the carbon-12 nucleus per nucleon is therefore (92.3 MeV)/(12 nucleons) = 7.69 MeV per nucleon


794