|
Kirchhoff’s first law provides relationships between the currents flowing into or out of a junction. By contrast, Kirchhoff’s voltage law, also known as Kirchhoff’s second law, relates voltages to one another. It states that the sum of the voltage differences (gains and drops) around a closed loop equals zero. This is much like saying that you add energy to an object when you lift it and get it back as you put the object back down. 
|
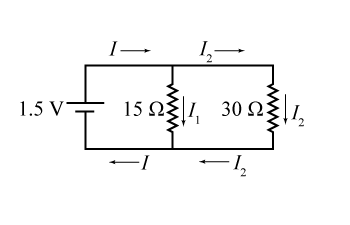How can we apply Kirchhoff’s second law to real-world design problems? Consider the now-familiar case of a parallel circuit with one battery and two resistors, shown at right. On page 490 we learned to apply Ohm’s law to each resistor separately so we could calculate each resistor’s current. Intuition then guided us to add the currents to get I.
|
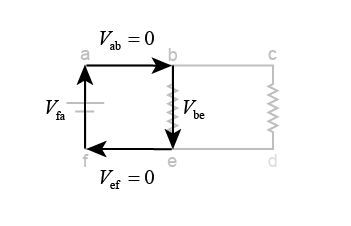Another approach is to look at the voltages across each element in a closed loop. One such loop, shown here, connects the battery to R1. The battery provides a voltage increase of 1.5 V, which must equal the voltage drop in R1, according to Kirchhoff’s second law. By applying Ohm’s law, that voltage drop must equal I1R1. Now we can solve for the current!
|
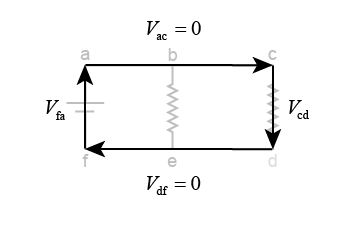Now take a look at the right-hand loop containing just the battery and R2. Here, too, the voltage drop I2R2 must equal the battery voltage of 1.5 V, according to Kirchhoff’s second law. Just as in the previous loop, the individual voltages add up to zero around any closed path that starts and ends at one point (such as f at right).
|
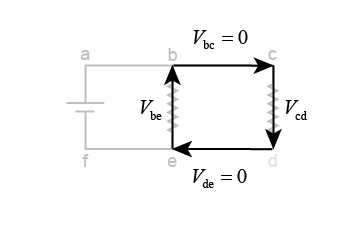Finally, Kirchhoff’s second law allows us to analyze closed loops that do not include any batteries. This enables us to quickly compare the relative amounts of current flowing through two resistors. In the example at right, the 15 Ω resistor will carry twice as much current as the 30 Ω one. Why? Both have the same voltage across them. Current is inversely proportional to resistance, so the resistor with half the resistance draws twice the current!
 |
Look carefully at the arrows in the final diagram. A closed loop requires one voltage drop to go in the same direction that current flows and another to go in the opposite direction. In the example shown, the upward arrow for Veb does not indicate the direction of current flow. Rather, current flows from top to bottom in both resistors. Since Vbe is a voltage drop, it follows that Veb is a voltage gain. 
|
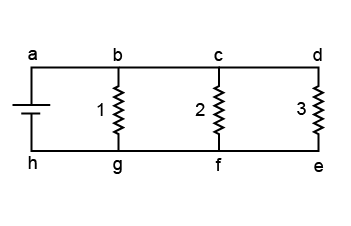A circuit featuring three resistors in parallel is shown here. Apply Kirchhoff’s second law on a simple closed loop, such as “a b g h a.” How many unique simple loops can be drawn on this circuit diagram? - 3
- 4
- 5
- 6
 |
The correct answer is D (there are six unique simple closed loops). The loops are as follows: - a b g h a
- a c f h a
- a d e h a
- b c f g b
- b d e g b
- c d e f c
|
