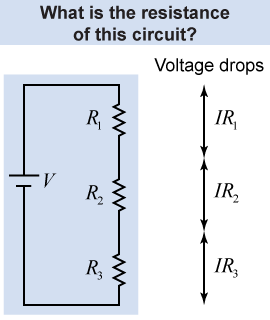Essential Physics

Resistors in series

What is the resistance of this circuit, consisting of three resistors in series?

Consider the circuit in the diagram that has three resistances and a battery connected in series.

How much current flows in this circuit?
How is Ohm’s law applied?

The answer is that the current in the circuit adjusts itself so that the sum of all the voltage drops equals the voltage provided by the battery. Since it is a series circuit, the current I is the same everywhere. In mathematics, the battery voltage V equals the sum of the voltage drops across each of the three resistances, R₁, R₂, and R₃:

V = I R_{1} + I R_{2} + I R_{3}

Read the text aloud

The current I in the circuit is the same through each resistor; therefore, we can rewrite this equation by grouping the resistances together as

V = I (R_{1} + R_{2} + R_{3})

Examine this equation and you will see that it looks just like Ohm’s law if we make the identification that the total resistance R of the circuit is equal to the sum of all the individual resistances:

R = R_{1} + R_{2} + R_{3}

This allows us to write the following for the total voltage and the total current:

\begin{matrix} V = I R, & I = \frac{V}{R} \end{matrix}

When two or more resistors are connected in series in a circuit, their total combined resistance is given by equation (17.3). The total resistance provides the easiest way to calculate the current in a series circuit. The current in the circuit is the total voltage divided by the total resistance. Read the text aloud

Read the text aloud

Show Voltage divider circuit

Voltage divider circuit

A frequently encountered circuit is the voltage divider. It is used to change the input voltage in a circuit, such as lowering the voltage when the power supply has a voltage that is too high for the operation of the circuit components.

In its simplest form, the voltage divider is a circuit with two resistors connected in series, such as the one shown here on the right. The total resistance of this circuit is R = R₁ + R₂. The current I is given by Ohm’s law:

I = \frac{V}{R} = \frac{V}{R_{1} + R_{2}}

The voltage drop V₂ across resistor R₂ is

V_{2} = I R_{2} = \frac{V}{R_{1} + R_{2}} R_{2}

And the voltage drop V₁ across resistor R₁ is

V_{1} = I R_{1} = \frac{V}{R_{1} + R_{2}} R_{1}

As an example, consider designing a voltage divider circuit to convert an input voltage of 9 V into an output voltage of 3 V. In order to have a potential difference of 3 V across resistor R₂, the ratio of the two resistors is

\frac{R_{2}}{R_{1}} = \frac{\frac{V_{2}}{V}}{1 - \frac{V_{2}}{V}} = \frac{\frac{3}{9}}{1 - \frac{3}{9}} = 0.5

Note that we only know the ratio of the two resistors, not the particular value of each resistor. If we want to set R₁ = 10 kΩ, then R₂ = 5 kΩ.

More generally, we cannot determine the best values for the two resistors because we do not have enough constraints in our system. In electronics, a typical constraint is a limit on the power dissipated by the circuit because we don’t want the resistors to overheat! We will learn more about power in electric circuits on page 494. Hide me!

Hide me!

(17.3)

R = R_{1} + R_{2} + R_{3} + \dots

R	=	equivalent resistance (Ω)
R₁	=	resistance 1 (Ω)
R₂	=	resistance 2 (Ω)
R₃	=	resistance 3 (Ω)

Equivalent resistance
series resistors

Two resistors with resistances of 10 Ω and 20 Ω are connected in series with a battery of voltage 10 V. What is the current through the circuit?

Asked:	total current I through the circuit
Given:	voltage V = 10 V; resistances R₁ = 10 Ω and R₂ = 20 Ω
Relationships:	Ohm’s law I = V/R; equivalent resistance for series resistors: R_eq = R₁ + R₂
Solution:	The equivalent resistance for the series circuit is R_eq = R₁ + R ₂ = 10 Ω + 20 Ω = 30 Ω The current is then $I = \frac{V}{R_{e q}} = \frac{10 V}{30 Ω} = 0.33 A$
Answer:	I = 0.33 A.

Read the text aloud

Seven resistors with resistances of 1, 2, 3, 4, 5, 6, and 7 Ω, respectively, are connected in series. What is their effective resistance? Show

Show

The resistors are connected in series; therefore, their resistances add directly when calculating the effective resistance:

\begin{matrix} R_{eq} & = & R_{1} + R_{2} + R_{3} + R_{4} + R_{5} + R_{6} + R_{7} \\ = & 1 Ω + 2 Ω + 3 Ω + 4 Ω + 5 Ω + 6 Ω + 7 Ω \\ = & 28 Ω \end{matrix}


488