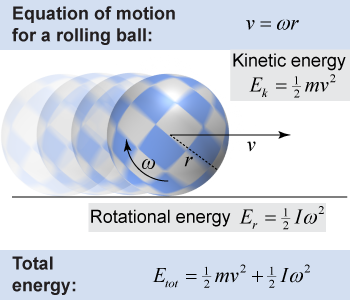|
When a ball rolls across the ground without slipping, the faster it moves across the ground, the faster it rotates about its center. The linear velocity v and angular velocity ω of a rolling ball are directly related to each other by the equation v = ωr, as we learned on page 207. Every time the ball rotates one complete turn (or 2π radians), it has moved forward by a distance of 2πr (the ball’s circumference). 
|
|
When the ball is rolling, it has both kinetic energy and rotational energy, which is sometimes called the kinetic energy of rotation. Linear kinetic energy is given by ½mv2, while rotational (kinetic) energy is given by ½Iω2. The equations look similar: You just substitute I for m and ω for v!
|
| (13.4) | | | Er | = | rotational energy (J) | | I | = | moment of inertia (kg m2) | | ω | = | angular velocity (rad/s) |
| Rotational energy
|
|
When a ball is rolling across the ground, it has both kinetic energy and rotational energy. Its total energy is the sum of the two: | |
How does the energy of a rolling ball compare with the energy of a skidding ball—i.e., a ball that is sliding across a frozen lake—moving at the same velocity? When the ball is sliding, it has no rotational energy, so its total energy is less than the rolling ball that moves at the same velocity.
|
Linear motion and rotational motion may appear different, but the mathematical representations for both are very similar. Whereas linear motion uses distances and velocities, rotational motion uses angles and angular velocities. Mass is used in linear motion but moment of inertia is used in rotational motion.
Comparison between linear and rotational motion | Linear motion | Rotational motion |
|---|
| Quantity | Variable or
equation | Units | Quantity | Variable or
equation | Units |
|---|
| Position | x | m | Position angle | θ | rad | | Velocity | v = Δx/Δt | m/s | Angular velocity | ω = Δθ/Δt | rad/s | | Mass | m | kg | Moment of inertia | I | kg m2 | | Momentum | p = mv | kg m/s | Angular momentum | L = Iω | kg m2/s | | Kinetic energy | Ek = ½mv2 | J | Rotational energy | Er = ½Iω2 | J |
 |
In more advanced physics courses, you will also study angular acceleration, which extends the analogy to linear motion. A more complete table of the comparison is given below. Comparison between linear and rotational motion | Linear motion | Rotational motion |
|---|
| Quantity | Variable or
equation | Units | Quantity | Variable or
equation | Units |
|---|
| Position | x | m | Position angle | θ | rad | | Velocity | v | m/s | Angular velocity | ω | rad/s | | Acceleration | a | m/s2 | Angular acceleration | α | rad/s2 | | Force | F | N | Torque | τ = Iα | N m | | Motion equations | v = Δx/Δt | m/s | Motion equations | ω = Δθ/Δt | rad/s | | v = v0 + at | m/s | | ω = ω0 + αt | rad/s | | d = ½at2 | m | | θ = ½αt2 | rad | | Mass | m | kg | Moment of inertia | I | kg m2 | | Momentum | p = mv | kg m/s | Angular momentum | L = Iω | kg m2/s | | Kinetic energy | Ek = ½mv2 | J | Rotational energy | Er = ½Iω2 | J | | Newton’s second law | F = ma | N | Newton’s second law
(rotational version) | τ = Iα | N m | 
|
A diver jumps off a diving board into the water without spinning, entering the water feet first. He then repeats the dive, but this time he does several somersaults before entering the water. If he followed the exact same trajectory in both dives, did his energy differ between the two dives? Explain.
 |
He had more energy during the second dive, because he had additional rotational energy. In both dives, he started with the same gravitational potential energy. But on the second dive he began rotating as he left the diving board. As a result, he started the second dive with both potential energy and rotational energy. 
|
