| | Essential questions | | Why does conservation of angular momentum cause objects to spin faster
or slower? | |
|
When an ice skater executes a spin, she will usually start with her arms and one leg extended. As she spins, she tucks in her limbs, causing her to spin faster. Why does this happen? In this investigation you will explore two similar examples where rotating objects speed up as the radius of rotation decreases. 
|
Part 1: Spinning in an office chair
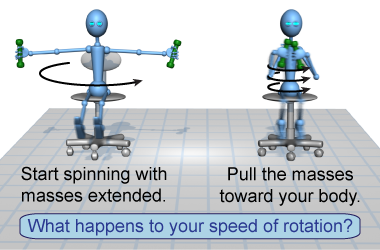
- Sit in an office chair that swivels, holding a small barbell (1–3 kg) in each hand.
- Spin yourself around with both arms outstretched.
- Pull your arms into your body.
- How does your angular velocity change as you pull your arms in or extend them?
- Why does this happen?

Part 2: Conical pendulum
 Safety warning: keep the pendulum bob away from people and objects that could be hit.
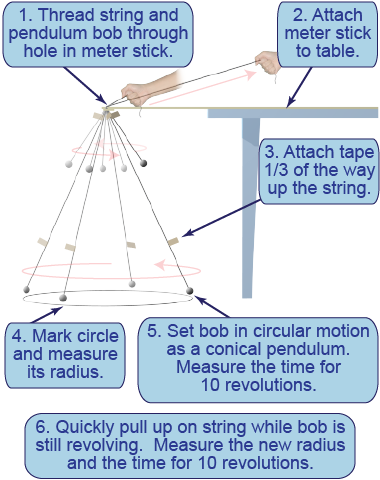
Safety warning: keep the pendulum bob away from people and objects that could be hit. - Attach a 1 m string to a pendulum bob and thread through the hole in one end of a meter stick.
- Attach the meter stick to a table with this hole extended away from the table.
- Attach a small piece of tape to the string approximately 1/3 of the distance above the pendulum bob.
- Mark a circle on the floor centered below the hole in the meter stick. Measure and record its radius.
- Gently set the bob in circular motion as a conical pendulum with a radius matching the circle. Measure the time for ten revolutions using a stopwatch. Calculate the angular velocity ωi.
- While the bob is still moving, quickly pull up on the string until the tape marker reaches the hole. Measure the new radius of the conical pendulum’s motion and the time for ten revolutions. Calculate the angular velocity ωf.
- How does the moment of inertia of the spinning bob change as you pull up on the string? Why?
- How does the angular velocity change as you pull up on the string? Why?
- Are your results (roughly) consistent with conservation of angular momentum? Explain.

|
|
Use this interactive utility as a stopwatch for this investigation.
|
Part 3: Spinning a mass overhead
 Safety warning: Attach the washer securely; keep the spinning washer away from other people; and do not spin it too fast, which can be dangerous.
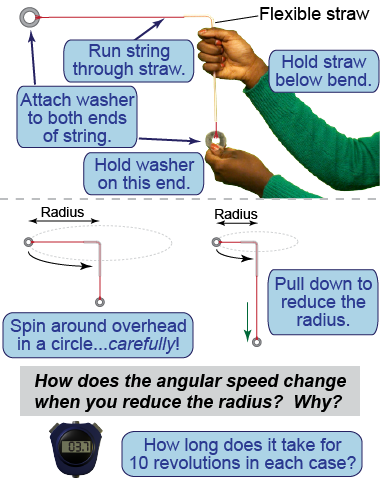
Safety warning: Attach the washer securely; keep the spinning washer away from other people; and do not spin it too fast, which can be dangerous. - Pass a string (approximately 1 m long) through a flexible straw and securely attach a washer to each end.
- Mark the string 10 and 50 cm from the lower washer. For each, measure the distance from the straw’s bend to the upper washer.
- While holding the straw and lower washer, spin the upper washer around overhead at constant speed.
- Using a stopwatch, measure the time for 10 revolutions when the string’s 10 cm mark lines up with the bottom of the straw, corresponding to a large radius of rotation. Calculate the angular velocity and tabulate with the radius of rotation.
- With the spinning washer moving at this initial angular velocity, quickly pull the lower washer down until the string’s 50 cm mark lines up with the bottom of the straw, corresponding to a small radius of rotation. Measure the time for 10 revolutions and calculate the angular velocity.
- How does the angular velocity change as you pull down the string? Why?
- By what factor did you change the radius of rotation? By what factor did the angular velocity change?
| |
| |
|

