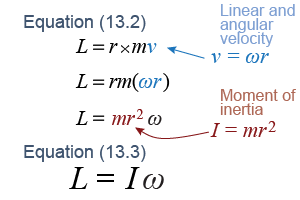|
Angular momentum obeys a separate conservation law from that of linear momentum. To best understand this conservation law we need to rewrite the equation for angular momentum. Recall that linear momentum is the product of mass and velocity, p = mv. We want a similar form of equation for the angular momentum in terms of the angular velocity ω. We start with equation (13.2) then use the fact that the linear velocity and angular velocity are related by v = ωr. 
|
|
If we regroup the terms, we find that the moment of inertia I in the angular momentum equation appears in the same place as the mass m in the linear motion equation. The result is equation (13.3), which tells us that angular momentum L is the product of moment of inertia I and angular velocity ω. Moment of inertia is the rotational analog of mass.
|
| (13.3) | | | L | = | angular momentum (kg m2/s) | | I | = | moment of inertia (kg m2) | | ω | = | angular velocity (rad/s) |
| Angular momentum
and moment of inertia |
|
Recall that Newton’s first law says the linear momentum of an object remains constant when the net force is zero. A similar rule holds for angular momentum.
The angular momentum of a rotating body remains constant when there is
zero net torque acting on the body.
|
|
Figure skaters and divers make use of angular momentum to perform feats of rotational agility. A skilled skater can increase her rate of spin to as much as five revolutions per second by pulling her arms close to her body. Platform divers tuck in their arms and legs while tumbling then open up their bodies to slow their rotation before hitting the water. Both techniques employ conservation of angular momentum.
|
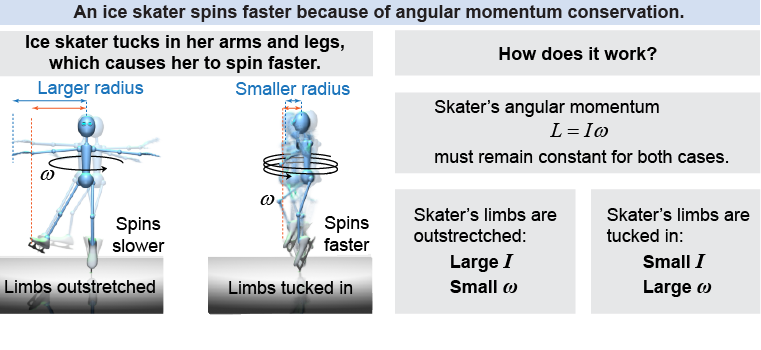
An ice skater sets up a fast spin by spinning slowly, with her arms and one leg extended. In the absence of any net torque, the skater’s total angular momentum is conserved. To spin faster, the skater reduces her moment of inertia I by pulling in her arms. To conserve L, her angular velocity ω increases!
 |
As you will learn in the next section, the ice skater’s moment of inertia is not exactly mr2, but it has a number less than one multiplied by mr2. Nonetheless, we are expressing her moment of inertia as mr2 to convey how her angular momentum L is varying with how far out (r) she stretches her arms. This is a simplification, indeed! 
|
|
When a platform diver wants to do a series of somersaults as part of his dive, why does he tuck his body into a tight ball?
 |
He tucks his body in tight to spin more quickly, because angular momentum is conserved while he spins in the air. By tumbling quickly, he can complete more somersaults before hitting the water and score higher on his dive! 
|
