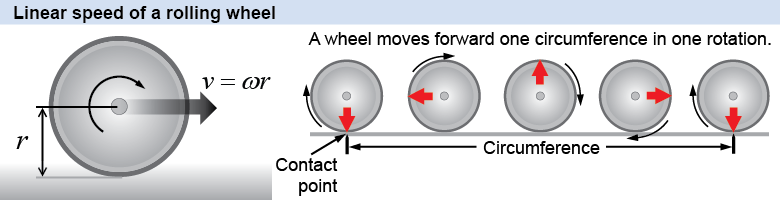
|
A rolling wheel has both linear and angular velocity. If the wheel is not slipping, the two velocities are related by geometry, because the circumference of a circle is 2π times the radius r. A wheel rotates through an angle of 2π radians (a full rotation) as it moves forward by a distance of 2πr (one circumference). 
| 
|
|
The linear velocity is the circumference divided by the time it takes to make one turn, i.e., v = 2πr/t. For one rotation, the quantity 2π/t is the angular velocity ω. The linear velocity is therefore equal to ω multiplied by the radius r. Linear and angular velocity are related to each other by the equation
|
| (7.2) | | | v | = | linear velocity (m/s) | | ω | = | angular velocity (rad/s) | | r | = | radius (m) |
| Linear velocity
from angular velocity |
|
The radius r that appears in equation (7.2) means that larger wheels have a higher linear velocity than smaller wheels for a given angular velocity. Early bicycles had very large wheels because the larger wheels would create a higher linear velocity. Unfortunately, they were very difficult to ride and quite unstable! Modern bicycles use gears and chains so that the pedals can turn at a different angular velocity from the wheels.
|
|
A car has wheels with a radius of 30 cm. What is the angular velocity of the wheels in both radians per second and revolutions per minute when the car is moving at 30 m/s (67 mph)? | Asked: | angular velocity ω calculated in two units: rad/s and rpm | | Given: | radius r = 0.3 m; velocity v = 30 m/s | | Relationships: | linear velocity v = ωr; one revolution is 2π = 6.28 radians | | Solution: | In rad/s, ω = v/r = (30 m/s)/(0.3 m) = 100 rad/s.
In rpm, ω = (100 rad/s)×(60 s/min)×(1 revolution/6.28 rad) = 955 rpm. | | Answer: | ω = 100 rad/s = 955 rpm |
|
A wheel is rolling at a linear velocity of 25 m/s. If the radius of the wheel is decreased, and the linear velocity remains the same, what does this indicate about the angular velocity of the smaller wheel? - It remains unchanged.
- It increases.
- It decreases.
- There is not enough information to answer.
 |
The answer is b. For a smaller wheel to move at the same linear velocity of a larger wheel, it must rotate faster. It will therefore have a higher angular velocity. 
|
