|
A rolling ball has both linear momentum and angular momentum. The linear momentum is the product of mass and translational velocity, as you learned on page 306. Angular momentum is a different kind of momentum, with different units that obeys a separate conservation law. Any moving mass has both angular momentum and linear momentum. The quantity of angular momentum depends on the choice of center of rotation as well as the mass and velocity. 
|
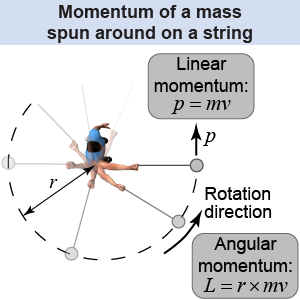Angular momentum is associated with the movement of mass about a particular axis of rotation. Imagine spinning a mass attached to a string around over your head. At any given moment, the mass m is moving with a velocity v, so it has a linear momentum p = mv. As it spins over your head, the same mass has an angular momentum (denoted with the letter L). Angular momentum is equal to the radius of rotation times the linear momentum, or L = r×mv. Note that the same mass moving at the same velocity may have a different angular momentum about a different center.
|
| (13.2) | | | L | = | angular momentum (kg m2/s) | | r | = | radius from axis (m) | | m | = | mass (kg) | | v | = | velocity (m/s) |
| Angular momentum
for a point mass |
|
Angular momentum and linear momentum have different units! The units of linear momentum are kg m/s. When we calculate angular momentum we multiply linear momentum by distance, so angular momentum has units of kg m2/s.
 |
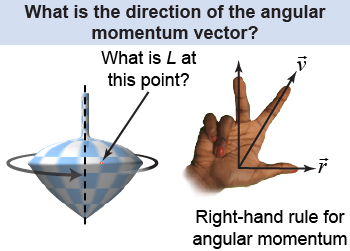In equation (13.2) above, we know that mass is a scalar quantity, but radius and velocity are vector quantities. Is angular momentum a vector quantity? Yes, as you will learn in a college-level physics course. The direction of angular momentum is perpendicular to both radius and velocity as given by the right-hand rule. What direction is the angular momentum vector for the spinning top shown in the illustration (at right)? Here's how to find out: Look at one small location on the surface of the top. Point your right thumb in the direction of the radius (from the axis to this location) and point your index finger in the direction of its velocity (tangential to the surface of the top). Your middle finger will now point in the direction of the spinning top's angular momentum vector, which is straight up!
What happens if you spin the top in the opposite direction? Use the right-hand rule again. Your thumb will be pointing in the same direction, but your index finger must now point in the opposite direction—the velocity points the other way because the top is spinning in the opposite manner. Your middle finger now points downward, which is the new direction of the angular momentum vector. 
|
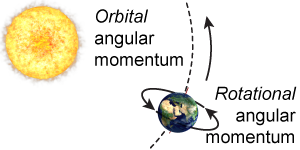An object can have multiple quantities of angular momentum around multiple axes. For example, Earth has rotational angular momentum because of its rotation about its north–south axis. Earth also has orbital angular momentum because the planet revolves around its orbital axis passing through the Sun.
|
Calculate the angular momentum of a 100 g mass revolving in a circle once per second at the end of a 0.75 m string. | Asked: | angular momentum L | | Given: | mass m = 100 g = 0.1 kg, radius r = 0.75 m, ω = 1 rev/s | | Relationships: | angular momentum L = rmv | | Solution: | The mass moves 2πr every second, so its velocity is v = distance/time = (2π)(0.75 m) ÷ (1 s) = 4.7 m/s
Its angular momentum is therefore L = rmv = (0.75 m)(0.1 kg)(4.7 m/s) = 0.35 kg m2/s | | Answer: | The angular momentum is 0.35 kg m2/s. |
|
If you double the mass of the object on a string that you are spinning around over your head, how will its angular momentum change?
 |
Angular momentum is L = rmv, which means that it is directly proportional to mass. Doubling the mass therefore causes the angular momentum to double. 
|
