Chapter 13 review

    Quantitative problems
      Section 13.1
      1. An object has a moment of inertia about an axis of rotation of I = 30 kg m2. What is its angular momentum L if it rotates with an angular velocity of ω = 2 s−1?

      2. Lizzie is spinning on a chair so that she has a moment of inertia of 10 kg m2. Her angular momentum is 5 kg m2/s.
        1. What is her angular velocity?
        2. If she withdraws her arms, making her moment of inertia 5 kg m2, what is her new angular velocity?

        3. Two skaters approach each other
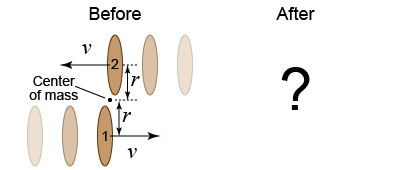
      3. Easy Two figure skaters of equal mass move toward each other, as shown here in this view from above. As they pass one another they join hands. Let v be the speed with which each moves upon the ice, and r the closest distance between each skater’s head and their shared center of mass.
        1. What is the total linear momentum of the pair before the skaters join hands? After?
        2. What is the total angular momentum of the pair before the skaters join hands? After?
        3. Use your answers to the previous two questions to qualitatively describe how the skaters would appear to move, as seen by a spectator.

        4. One skater traveling at 2<i>v</i> and the other motionless then lock hands side-by-side
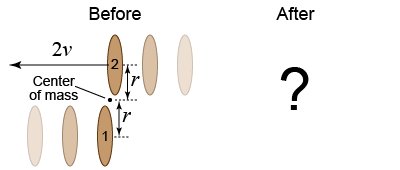
      4. Medium Two equally massive skaters face each other on the ice. Skater 1 is motionless and Skater 2 approaches with a speed of 2v. The skaters join hands when Skater 2 reaches Skater 1.
        1. What is the skaters’ total linear momentum before joining hands? After?
        2. What is the skaters’ total angular momentum before joining hands? After?
        3. Use your answers to the previous two questions to qualitatively describe how the skaters would appear to move from a spectator’s point of view.

      1. Medium A 1,000-kg communications satellite orbits the Earth at an altitude of 500 km, completing one revolution every 90 minutes. What is its angular momentum? (The Earth’s average radius is approximately 6,400 km.)

      Section 13.2
      1. A solid, 50 kg cylinder with a radius of 0.25 m is rotating with an angular velocity of 60 s−1.
        1. How much rotational energy is stored in this rotating cylinder?
        2. If that energy could be entirely used to lift the cylinder, how high would it go?

      2. An engineer wishes to modify an existing flywheel design so that the device can store more rotational energy. Which of the following changes will increase rotational energy by the largest factor? (The original design calls for a solid, 50 kg cylinder with a radius of 0.5 m, rotating with an angular velocity of 60 s−1.)
        1. increasing the radius to 0.75 m
        2. increasing the mass to 100 kg
        3. replacing the solid cylinder with a hollow cylinder and reducing the mass to 25 kg
        4. doubling the angular velocity


      3. Easy For which of the following astronomical motions is the amount of rotational energy the greatest: the Earth’s rotation about its axis or the Moon’s revolution about the Earth?
        The mass of the Earth and Moon are 6.0×1024 kg and 7.3×1022 kg, respectively. The radius of the Earth is 6.4×106 m. The Moon’s orbital radius is 3.9×108 m. (Assume that the Moon completes one revolution every 28 Earth days and that the Earth is a solid sphere of uniform density.)

      4. Medium Suppose that a sphere or cylinder is released from rest at the top of a ramp. At the top, it has a gravitational potential energy of mgh. When it reaches the bottom, this energy will be converted entirely to kinetic energy and rotational energy (assuming friction and air resistance are negligible). For each of the following shapes, what fraction of the original potential energy becomes rotational energy?
        1. solid sphere
        2. hollow sphere
        3. solid cylinder
        4. hollow cylinder

      384 Previous Page Next Page