Chapter 13 review

    Conceptual questions
      Section 13.1
      1. If you double an object’s rotational speed, what happens to its angular momentum?

      2. A small, dense object is spun around on a string at 10 m/s. If you triple the length of the string (the radius of the object’s “orbit”) without changing the speed, what happens to the object’s angular momentum?

      3. A ferris wheel takes a long time to get up to speed. If you double its radius without changing its mass or engine, will it take more or less time to get up to speed? Explain.

      4. Which is easier to balance, a carrot with its thick end up or a carrot with its thick end down? Explain.

      5. Easy The radius r in the equation L=r×mv refers to
        1. the minimum radius of the object.
        2. the maximum radius of the object.
        3. the distance between mass element m and the axis of rotation.
        4. the distance from the axis of rotation to the outermost part of the object.


      6. An object orbits the Earth at a radius beyond the Earth’s atmosphere.
        1. What force keeps the object from flying off into space?
        2. Does that force exert any torque?
        3. Is the object’s angular momentum conserved?

      7. A figure skater jumps into the air and contracts her arms so that her spinning speeds up in midair.
        1. Does her angular velocity change?
        2. Does her moment of inertia change?
        3. Does her angular momentum change?
        4. Does she exert any torque?

      8. Easy When you pick up a heavy object, why do you usually lean your torso backward?

      Section 13.2
      1. Why would toymakers build children’s tops with relatively large moments of inertia, even though a large moment of inertia makes it harder to start something spinning?

      1. Jeremiah has a thin metal hoop and a solid metal disk, each 40 cm in radius. Suppose that he conducts an experiment and finds that their moments of inertia are equal. Which object is heavier?

      2. Easy Suppose that Eleftheria has two metal disks, each with a radius of 40 cm and a mass of 400 g. An experiment reveals that Disk A has a greater moment of inertia than Disk B. What does this prove?

      3. A spinning gyroscope wheel completes 10 full rotations per second. Suppose that the rate is increased to 20 rotations per second. By what factor does that multiply the wheel’s rotational energy?

        4. Revolving doors with three glass panels 120° apart
      4. A revolving door generally consists of three glass panels 120° apart, all attached to a central axis and revolving within a partial cylinder. Visitors must step into the space between two panels and push on one in order to pass through the door. State one possible advantage and one possible disadvantage to building a revolving door with a large moment of inertia.

        5. Meter stick with lumps of clay at each end
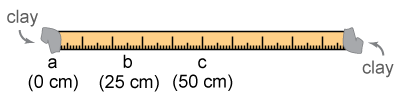
      5. A student has attached two equally massive lumps of clay to opposite ends of a lightweight but stiff meter stick. She plans to twirl the stick end over end while holding it at each of the three labeled positions. Which position will be easiest to twirl? Hardest? (Assume that the mass of the meter stick itself can be ignored.)

      6. Easy Suppose a ball is placed at the top of a ramp and released from rest. It rolls to the bottom in 2 s. Next, the ramp is lubricated and the ball is released from the top once more. This time, it slides to the bottom without spinning. Will it take less than 2 s, more than 2 s, or 2 s to reach the bottom this time?

      Previous Page Next Page383