|
Design a solar power array for the roof of a house that: - is sited at the latitude of your school, city, and/or town;
- generates an average of 50 kWh per day, equivalent to 18,000 kWh per year (the average energy consumed by a household);
- pays for itself within five years, compared to the cost of grid power of $0.12/kWh; and
- delivers a peak energy of 70 kWh per day in July in order to run the house’s air conditioning.
Designs are evaluated based on achieving these criteria at the lowest total cost. 
|
What is the need or problem that is addressed with a household solar power array? Which design criteria are the most important to meet? Write your explanations in your report.
 |
The average household in the USA uses 18,000 kWh per year of energy. Around 6,000 kWh of that amount consists of electrical energy for major appliances, lights, electronics, and so on that are powered from the electrical grid. The other 12,000 kWh is the equivalent energy that is typically used by heaters (space heaters or a water heater) that are typically powered by natural gas or home fuel oil. A complete solar power installation would replace not just the electrical grid power but also the energy needed to heat water and heat the house. 
|
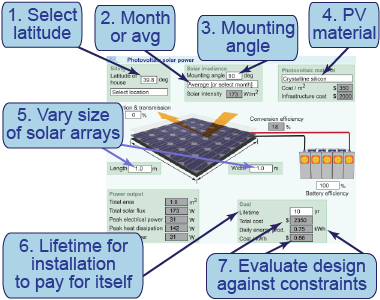In this interactive simulation, you will design a solar power system by modifying (and improving) an existing design that uses photovoltaic cells. Some of the parameters are fixed by typical commercial value: cost for PV arrays ($300/m2); installation cost for electrical hookups, such as the charge controller and grid-tie inverter ($3,000); conversion efficiency from incident light into electrical energy (18%); and battery storage efficiency (100%). Because this is a simulation, the design process will not include the engineering process step of prototyping your design.
|
Formulate testable hypotheses to address the first three design constraints. The parameters that should be varied are area (length and width) of the PV cells, mounting angle for the installation, month or year (start by using “Yearly Average”), and lifetime of the installation.
|
|
In this simulation, you can vary the design parameters to determine how to optimize them. Change the design parameters to maximize or minimize the key design criteria: daily power production (in kWh), cost per kWh, and total cost.
|
|
Analyze your data to determine which solutions best meet the first three design criteria. Write down the parameters of your design and the resulting key design elements.
|
|
Now look at the power production for the month of July. Does your design meet the last of the four design criteria? If not, revise your design to improve it to meet this last criterion. How did your design change? Make a short presentation to your class of your final design along with data to support your design decisions. As a class, discuss the best design elements. Revise your design to incorporate any elements you might have missed.
|
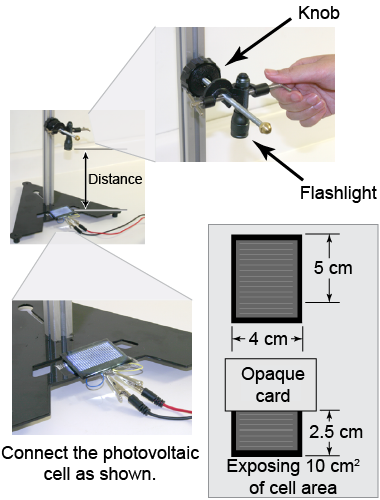Measure the voltage of a photovoltaic cell - Place the photovoltaic cell on the base of the stand. Connect the red and black leads from the ErgoDAQ (or a digital multimeter) to the cell.
- Using the stand, mount the flashlight pointing downward an initial distance of 10 cm from the cell.
- Measure the voltage detected across the photovoltaic cell.
- Cover half of the photovoltaic cell and measure the voltage again.
- Observe how the voltage varies while you tilt the photovoltaic cell progressively more and more relative to the horizontal.
- With the photovoltaic cell horizontal and uncovered again, measure the voltage across it for four other distances between the flashlight and the cell.
- How does the voltage across the photovoltaic cell change when you covered half of the cell? Why do you think that happens?
- How does tilting the cell change the voltage you measure across it? Explain why you think this happens and how the energy of a roof’s solar power array will vary with the slant of the roof.
- How does the photovoltaic cell’s voltage vary with distance from the flashlight? What is the functional form (e.g., linear, parabolic, inverse, etc.) for the dependence of voltage on distance?
|
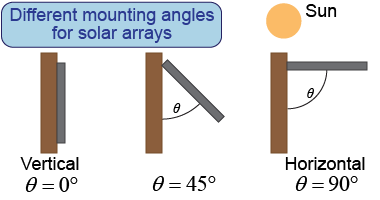
Santos Claughs has a house at the North Pole and wants to mount a solar array on his house to defray some of the cost of his home heating bill. What is the optimal mounting angle he should use for the solar panels? Why?
 |
He should mount them with an angle of around 90°; i.e., the panels should be vertical, facing sideways. The yearly average vertical position of the Sun is approximately the horizon, so that is where the panels should be facing. (A better answer is that they should be pointed around 12° above the horizon, because the position of the Sun when it is above the horizon—and can be seen—is between 0° and 23°.) 
|
Design project: Solar power
