|
How do you get time from speed and distance? The answer is to “solve” the equation for time. “Solving for t” means rearranging the equation into the form t = ? in which “?” are the other variables and there are no t’s on the right of the equals sign. Using the rules of algebra, we can restate the same relationship as t = d ÷ v or as d = vt. 
|

|
The general equation (d = vt) must be applied to the specific speed, time, and distance variables for your problem. Let’s look at the equation for bicycle 1. We write the speed equation as d1 = v1t1. We do a similar thing for bicycle 2 to get a second equation d2 = v2t2. 
|
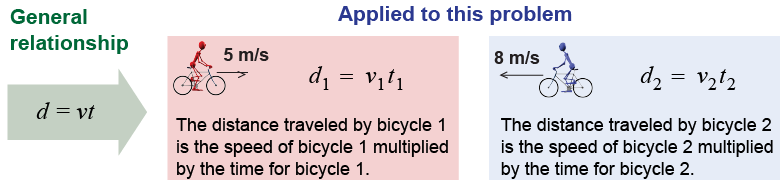
|
We are given that v1 = 5 m/s. We do not, however, know the distance d1, so we cannot calculate a time. We have the same problem with the equation for bicycle 2. This brings up an important rule.
One equation allows you to determine only one unknown value.

|
Looking at this problem, we see that there are four unknown values: t1, t2, d1, and d2. It is a fundamental rule that you need as many equations as you have unknown values. Four unknowns means that we need four equations to solve the problem. We have two equations; we need two more. 
|

|
A physics student sits down to solve a hard problem, deriving seven different equations that contain six unknown quantities. Is it possible for her to find a unique mathematical solution to the problem?
 |
Yes, there is a unique solution as long as the number of independent equations (seven) is equal to, or greater than, the number of unknown quantities (six). 
|

