|
|
There are forms of potential energy other than gravitational. Potential energy exists any time a force is restrained from acting in such a way that the energy can be released if the restraint is removed. If you use the spring to launch a marble you can see how the stored potential energy of the spring is converted to kinetic energy of the marble. Compressing a spring creates potential energy because you have to do work against the force of the spring to compress it. A compressed spring stores potential energy as long as it is compressed. This type of potential energy is called elastic potential energy because it derives from the elasticity of the steel in the spring. It can be calculated by using equation (9.4). 
|
| (9.4) | | | Ep | = | elastic potential energy (J) | | k | = | spring constant (N/m) | | x | = | displacement from equilibrium (m) |
| Elastic potential energy
|
|
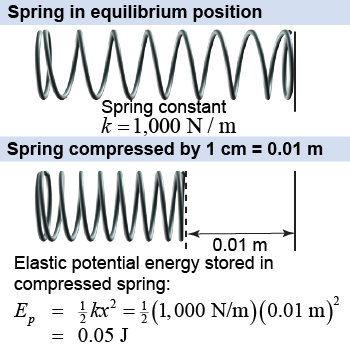The quantity k in equation (9.4) is called the spring constant, which represents the strength of the restoring force exerted by the spring when it is compressed or stretched. The spring constant is a property of the spring itself and is different for every spring or other elastic material. It has units of force divided by distance, because the spring exerts a restoring force that increases as the spring is increasingly displaced (stretched or compressed) from its equilibrium position. A stiff spring resists compression or stretching, so it has a large value of the spring constant k; a loose spring has a low value of k.
 |
The restoring force for a spring is directly proportional to the distance the spring is stretched from its relaxed state. This simple relationship is called Hooke’s Law and is mathematically expressed as | | | F | = | restoring force (N) | | k | = | spring constant (N/m) | | x | = | displacement from equilibrium (m) |
| Hooke’s law for springs
|
The force F is the restoring force that acts to move the spring back to its unstretched and uncompressed position. The negative sign in the equation tells you that the restoring force acts in the opposite direction from the displacement; i.e., as you stretch out the spring in one direction, the restoring force pulls against you in the opposite direction. 
|
|
Objects that store elastic potential energy share some common features: Energy is stored when the object changes its form, shape, or length; the force exerted by the elastic object acts in a direction to return it back to its original shape or position; and as it stretches or compresses more, it stores more energy.
|
|
The biceps and triceps muscles in your arm work the same way: When you flex your arm, the biceps muscle contracts as it releases its stored elastic potential energy; at the same time, the triceps muscle is stretched, storing up elastic potential energy. The arm extends by contracting the triceps muscle and releasing its stored energy; at the same time, the biceps muscle is stretched, storing energy. The biceps and triceps muscles work in tandem: One contracts, releasing energy to move the joint, while the other is stretched, storing energy. Every joint in your body moves in a similar way, using opposing pairs of muscles that exert force by contracting.
|
|
|
|
|
Springs and rubber bands also store elastic potential energy when stretched. The stored energy is then released when the spring contracts back to its original shape. A spring is often used in a screen door closing mechanism; when you open the door the spring is stretched, and the spring contracts to close the door when you let go. A bow works by storing energy as an archer pulls back its drawstring and deforms the bow; when the archer lets go, the potential energy of the bow is converted into kinetic energy of the arrow. As you land on a trampoline it stretches downward and stores elastic potential energy, which it then releases by bouncing you back up into the air. A thin sheet of metal that is bent stores elastic potential energy, which it releases when it quickly snaps back into shape.
|
Which has a greater spring constant value, a Slinky® or a car’s suspension spring?
 |
A car’s suspension spring has to exert a much greater force per unit of distance compressed than a Slinky®, so it has a greater spring constant. 
|
