|
Potential energy is the energy of position. The word “potential” describes the fact that potential energy is not active. It is stored energy that has the ability to become active. A good example is to compare the energy of a brick on the table to that of a brick on the floor. By virtue of its being higher than the floor, the brick has more potential energy when it is on the table than it does when it is on the floor. The brick on the table, however, is not using its energy by moving, heating up, or doing anything else. 
 |
There are many other mechanisms by which different kinds of potential energy are stored. A rubber band stores elastic potential energy when it is stretched, then releases the stored energy when the rubber band reverts to its original shape. A battery stores electric potential energy, which can be released by connecting it to a circuit and allowing electric current to flow. A hydroelectric dam stores gravitational potential energy in the water behind the dam, which is converted to mechanical energy and then electrical energy when it flows down through the turbines. Chemical bonds between molecules in a solid store chemical potential energy. Chemical potential energy may be released during chemical reactions such as when hydrogen and oxygen react to form water. 
|
|
How much potential energy does the brick have? If the brick has more mass, the force of gravity gives it more weight and more potential energy. If it has more height, it can fall farther and also has more potential energy. By these arguments we deduce that potential energy depends, at least, on weight and height. Checking the units supports that conjecture—the product of weight times height has units of force times distance, the same as work. The equation for gravitational potential energy (Ep or PE) is exactly what we surmised. The potential energy of any object of mass m raised by a height h is given by equation (9.3).
|
| (9.3) | | | Ep | = | potential energy (J) | | m | = | mass (kg) | | g | = | acceleration of gravity | | h | = | change in height (m) |
| Gravitational
potential energy
|
|
|
Potential energy exists because there is a force that we must work against to raise the brick from the floor to the table. In this case the force we must work against is gravity. Gravity still acts on the brick once it is on the table and therefore the work we do to raise the brick is stored as potential energy, which can be recovered by letting the brick fall back down again. An important concept is that potential energy represents stored work that may be recovered when the energy becomes active—such as by changing an object’s height.
|
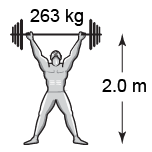The current weightlifting world record of 263 kg was set by Hossein Rezazadeh of Iran in 2004. (a) How much gravitational potential energy did the barbell have if he held it 2.0 m above the floor? (b) How much work did he perform to lift the barbell from the ground to the overhead position? | Asked: | (a) potential energy Ep of the barbell overhead and
(b) work W done by the weightlifter to lift the barbell overhead from the floor | | Given: | barbell mass m = 263 kg, barbell final height h = 2.0 m | | Relationships: | Ep = mgh, g = 9.8 m/s2 | | Solution: | (a) Ep = mgh = (263 kg)(9.8 m/s2)(2.0 m) = 5,155 J.
(b) As given in Part (a), the change in potential energy of the barbell from the floor (Ep = 0) to its overhead position is 5,155 J. The minimum work done by the weightlifter is the same as the change in PE. | | Answer: | (a) Gravitational PE is 5,155 J; (b) minimum work done is 5,155 J. |
|
If a 14 kg box is raised to a height of 4.0 m on Earth, what is its gravitational potential energy relative to the ground? - 550 J
- 56 J
- 3.5 J
- 0.29 J
 |
Asked: gravitational potential energy Ep of the box
Given: box mass m = 14 kg; box final height h = 4.0 m;
acceleration due to gravity g = 9.8 N/kg
Relationships: Ep = mgh
Solve: 
|
