|
|
A dynamics problem involves accelerated motion and force. In dynamics problems, the second law is used to calculate the acceleration and resultant motion of an object from a known mass and known forces. For example, the acceleration of a rocket can be calculated from the thrust force of the engines and the mass of the rocket.
|
- The acceleration is always in the direction of the net force.
- Consistent units must be used for force, acceleration, velocity, distance, and time.

|
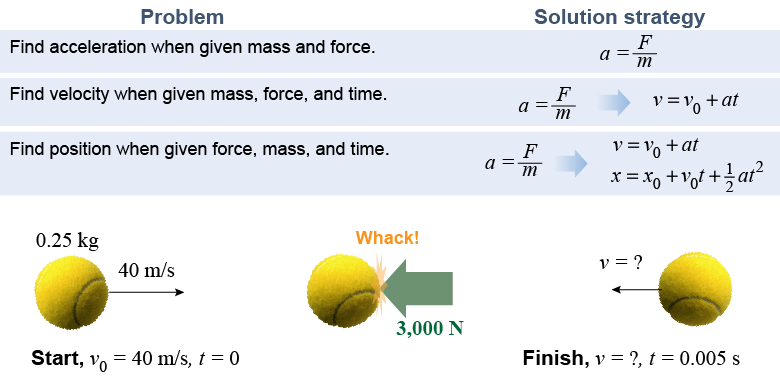
|
A 250 g ball traveling to the right is hit by a racquet, which applies a force of 3,000 N to the left for 0.005 s. What is the velocity of the ball afterward? | Asked: | final velocity v of the ball | | Given: | m = 0.25 kg, v0 = +40 m/s, t = 0.005 s, F = −3,000 N | | Relationships: | a = F/m, v = v0 + at | | Solution: | Find the acceleration: a = F/m = (−3,000 N) ÷ (0.25 kg) = −12,000 m/s2 Find the final velocity: v = v0 + at = (40 m/s) + (−12,000 m/s2)(0.005 s) = −20 m/s | 
|
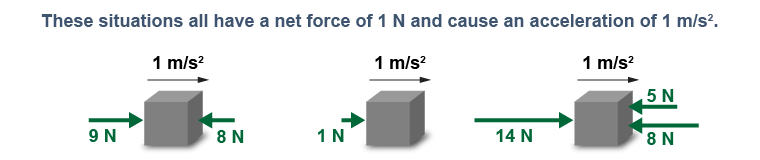
In many problems you will see terms such as “minimum force” used. The word “minimum” is there because it is always possible to have a larger force acting partially in the wrong direction. The minimum force required to accelerate a 1 kg object at 1 m/s2 is 1 N. No net force smaller than 1 N can cause this acceleration. You could, however, apply a 100 N force and still have a net force of 1 N if there were other forces acting, such as friction or normal forces. 
|
|
A net force of 100 N acts on a cart with a mass of 5 kg. Determine the acceleration of the cart if the cart is free to move with no friction.
Which of the following relationships would be useful in solving this problem, involving what is asked and what is given? - a = F/m
- Fnet = F1 + F2 + F3 + ⋯
- v = v0 + at
- τ = F × d
 |
The answer is a. The question provides the force and mass, and you are asked for acceleration. Only a represents a relationship among these three variables. By the way, the solution is 
|
| |
|

