|
A good example of determining force from motion is the specification of aircraft engines. An aircraft must reach a minimum speed to take off and fly. The mass of the plane is known. The runway length is also known, as is the maximum comfortable acceleration for passengers. Newton’s second law is applied to calculate how much thrust force must be supplied by the engines. 
|
|
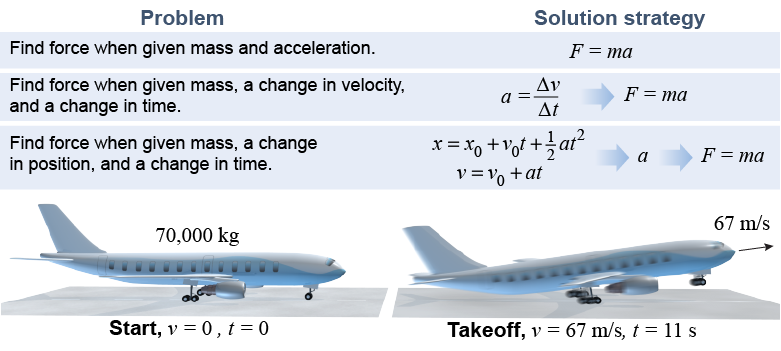
A 70,000 kg aircraft reaches a takeoff velocity of 67 m/s (150 mph) in 11 s. Calculate the minimum force required from the engines. | Asked: | force F | | Given: | m = 70,000 kg, vf = 67 m/s, and t = 11 s | | Relationships: | F = ma, a = Δv/Δt | | Solution: | Find acceleration first: a = Δv/Δt = (67 m/s)÷(11 s) = 6.1 m/s2
Next, find force: F = ma = (70,000 kg)(6.1 m/s2) = 427,000 N | | Answer: | 427,000 N |
|
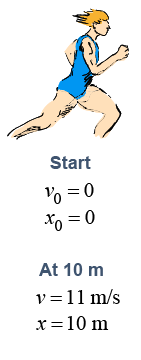A 65 kg sprinter reaches a maximum speed of 11 m/s at a distance of 10 m from the start of a race. What average force must the sprinter’s muscles create? | Asked: | force F | | Given: | m = 65 kg, vf = 11 m/s, and x = 10 m | | Relationships: | F = ma, x = x0+ v0t + ½at2, v = v0 + at | | Solution: | Use both motion equations to find acceleration first:
v = v0 + at → t = v/a
x = x0 + v0t + ½at2 → x = ½at2
x = ½a(v/a)2 → x = v2/2a
a = v2/2x = (11 m/s)2 ÷ (2)(10 m) = 6.05 m/s2
Next, find force:
F = ma = (65 kg)(6.05 m/s2) = 393 N | | Answer: | 393 N |
|
| |
|
