|
A straight, current-carrying wire in a uniform magnetic field can experience a magnetic force, as we learned on the previous page. What happens if the wire is twisted into a loop or coil? (This is often called a current loop.) This is the principle behind a number of useful devices, such as the generator and the galvanometer. 
|
|
|
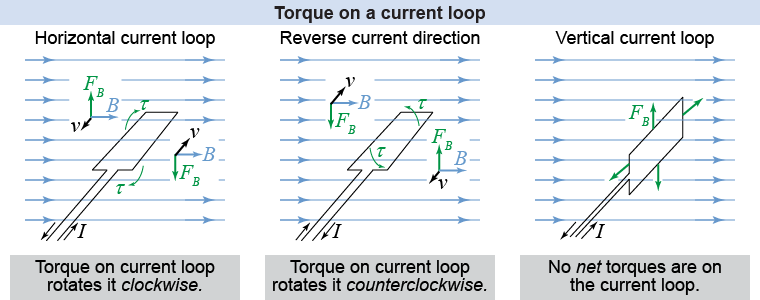
Let’s start with the situation where the plane formed by a rectangular current loop is parallel to the direction of the magnetic field, as shown in the left-hand panel of the figure above. The current through the loop, shown in the figure, causes the right side of the loop to experience a downward magnetic force—by the right-hand rule on page 561. The left side of the loop, however, experiences an upward force because the current (and electric charge) flows in the opposite direction. These two forces create torques that will rotate the current loop clockwise! If the current is reversed, as in the middle figure, then the forces are reversed and the torque rotates the loop in the opposite, counterclockwise direction.
|
|
A current loop in a uniform magnetic field may feel a torque—but not always! In the right-hand figure above, the plane of the current loop is perpendicular to the direction of the magnetic field. Now each segment of the rectangular loop experiences a force—but in outward directions. Each of the opposite forces cancel, resulting in no net force or torque. The loop is in equilibrium!
|
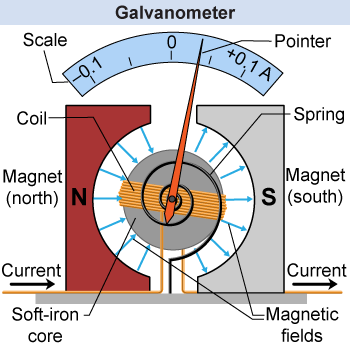The current loop in a magnetic field rotates in a manner that depends on the direction of the current flowing through the loop. This is the principle behind a scientific instrument called the galvanometer. A galvanometer detects and measures the current flowing through a wire using the rotation of the wire loop in a uniform magnetic field. A small spring is often mounted on the loop to keep it at the zero position when no current is flowing. A galvanometer can be used as an ammeter and can be a sensitive detector of small currents.
|
In the right-hand panel of the top illustration on this page, the current loop experiences no net force or torque. Is this stable or unstable rotational equilibrium?
 |
It is a stable equilibrium. If the loop is rotated a small amount out of the equilibrium position, the loop experiences torque that acts to return the loop to the equilibrium position, which is the condition of stable equilibrium. 
|
