|
The Stefan–Boltzmann relation tells half the story by giving the emitted power in radiation. In reality, every object that emits radiation also absorbs radiation emitted by other objects in the environment. Radiative heat transfer depends on the difference between energy absorbed and energy emitted. In general, this is very complicated because exact shapes and positions matter in determining how much radiation emitted from one object is absorbed by another. Nevertheless, a useful simple case occurs when an object is surrounded by an environment at a constant temperature. The net power exchanged by radiation between a body at one temperature and the environment at a different temperature is given by equation (24.4). 
|
| (24.4) | | | P | = | power (W) | | ε | = | emissivity (dimensionless) | | σ | = | Stefan–Boltzmann constant
= 5.67×10-8 W m−2 K−4 | | A | = | emitting surface area (m2) | | T∞ | = | environment temperature (K) | | T | = | object temperature (K) |
| Radiant
heat transfer
|
|
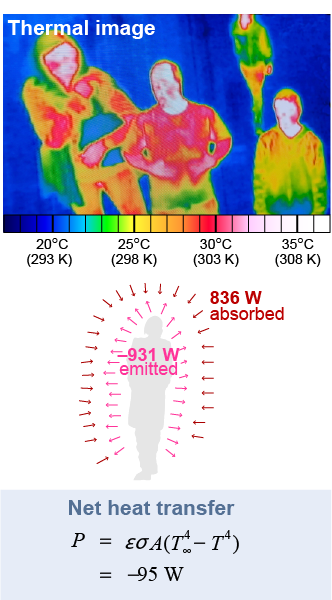
The radiative heat transfer from a human body makes a good example. The surface area of an adult is around 2 m2. Assume skin has an emissivity of 1 since only transparent, metallic, or reflective surfaces have emissivities much lower than 0.9. When the room is at 20ºC (68ºF) the average surface temperature of a person’s clothing is about 28ºC or 301 K, as shown by the thermal infrared camera image on the right. An infrared camera “sees” in infrared then electronically converts the infrared to colors to represent temperature. 
| 
|
The radiation emitted from 2 m2 at 301 K is 931 W. The same surface absorbs 836 W from the room radiating back at 293 K. The net heat transfer is just under 100 W. Humans radiate about 100 W constantly just by being alive! If you evaluate this heat loss over 24 hours it comes out to 8.2 MJ of energy, or 1,960 calories, the approximate energy equivalent of three meals. 
|
The temperature of any object reflects the balance of heat gained and heat lost. If more heat is gained, temperature increases. Increased temperature, in turn, means heat is lost more rapidly. In a steady state situation, the temperature comes to equilibrium at just the point where the heat lost through all mechanisms (conduction, convection, and radiation) equals the heat absorbed. 
|
| |
|

