|
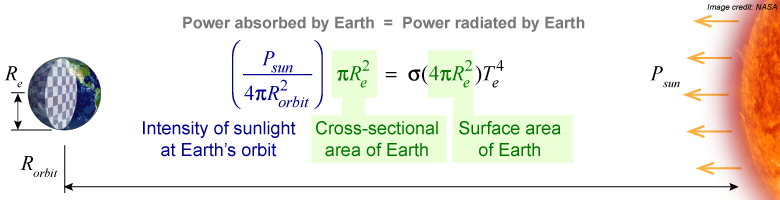
Earth is isolated in space, far from any source of significant thermal radiation except for the Sun. Earth’s temperature is a balance between radiant energy absorbed from the Sun and energy radiated away into the cold of space. For a simple and surprisingly accurate model for the temperature of our planet, we can assume that the solar energy absorbed by Earth’s disk, with an area of πRe2, is radiated back into space over the entire surface area of the planet, 4πRe2. 
|
|
The Sun’s power Psun is spread out over a sphere of radius Rorbit. The amount of power intercepted by Earth is on the left of the equation above. On the right is the radiated power of Earth with an average temperature Te and emissivity ε = 1 assumed. Notice that Earth’s radius Re cancels from both sides. After taking the fourth root to solve for the temperature, we have a single equation model that predicts the average temperature of a planet given only the power of the Sun and the planet’s distance from the Sun. 
|

|
The average surface temperature of Earth is 287 K (13ºC). The average temperature of the atmosphere and clouds is slightly lower, in excellent agreement with this model. The model is accurate because a planet such as Earth has been in existence long enough to come to steady-state equilibrium with regard to energy balance. The same is true for other celestial bodies that are not stars, including comets, asteroids, and moons. The temperature of each is set by the balance of radiative heat transfer. One astronomical unit (AU) is equal to Earth’s orbital radius. When the radiative balance model is written in astronomical units the result is a simple but very accurate way to estimate the average temperature of any body in the Solar System! 
|
| | | T | = | absolute temperature (K) | | R | = | orbit radius (AU) |
| Average temperature
of an object in the Solar System
|
|
Estimate the average temperature of Saturn, which has an orbital radius of 9.6 AU. Compare this to the observed temperatures of between 84 and 134 K at different levels of Saturn's atmosphere.
 |
This is within the range of observed measurements. In fact, this temperature represents the depth in Saturn's atmosphere at which the gases are dense enough to become opaque. 
|

