|
| Essential questions | | How can a lever be used to multiply force?
How does the work done vary with levers? | |
|
The lever is a simple machine with many applications. The most common use is to lift heavy objects, but not all lever designs increase the force applied! In this investigation you will use a see-saw to determine the ways in which a lever can be used to increase force. 
|
Part 1: Applying force to the opposite end of the lever
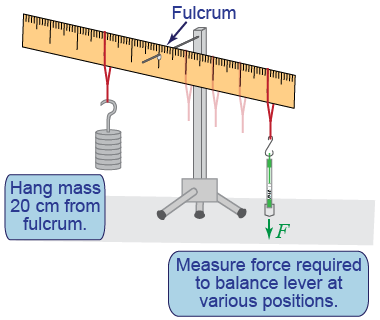
- Use the spring scale to measure the weight of the mass provided.
- Hang the mass 20 cm from the fulcrum on one side of the meter rule.
- Using the spring scale, balance the “see-saw” by pulling the meter rule at various places (between 10 and 40 cm) on the side opposite the mass.
- In each case, measure the force F on the spring scale and the distance d between the spring scale and the fulcrum. Tabulate your results.
- Double the mass of the hooked and slotted masses. Repeat the measurements of the previous step and tabulate your results.
- What is the value of the gravitational force exerted by the hanging mass?
- At what distances from the fulcrum does it take less force to balance the see-saw than the force exerted by the hanging mass?
- How did the force applied by the spring scale vary when you doubled the value of the suspended masses? Why?

|
Part 2: Applying force on the same end of the lever
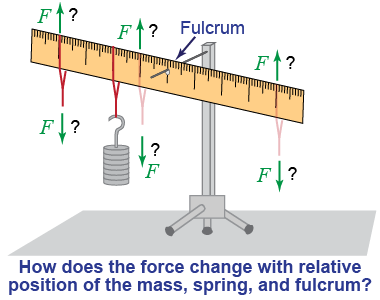
- Repeat the experiment, but now use the spring scale to pull on the meter rule on the same side as the hanging mass. Tabulate your results.
- How are the forces applied different from the forces applied in the first part? (
Hint: Force is a vector!) For this part and the previous one, draw diagrams to describe the three different configurations for the relative positions of the fulcrum, applied force (“effort”), and resistance force (“load”). 
|

