- A small house is in thermal equilibrium at noontime on a cold, winter day. The furnace generates 1,500 W of heat, while the walls conduct and convect 1,800 W away from the house. How much thermal radiation from the Sun is helping to warm the house?
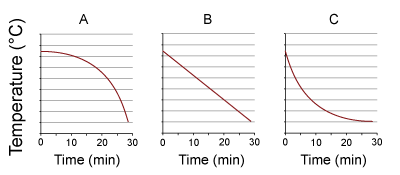
- According to Newton’s cooling law, the rate at which a substance cools is proportional to the difference in temperature between that substance and its surroundings. If that is true, which one of these three curves best represents a cup of coffee that cools from brewing temperature to room temperature?
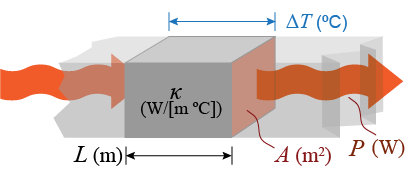
 A temperature difference of ΔT exists between the inside (left) and outside (right) of a building. The wall has a thickness L. Thermal energy is conducted at a rate P through a section with area A. The wall material has a thermal conductivity κ.
- If ΔT = 20°C, L = 40 cm, and κ = 0.3 W/(m °C), how many watts of thermal energy will flow through each square meter of the wall?
- Now suppose that ΔT = 20°C and L = 40 cm, as before, but 30 W of thermal energy flows through each square meter of the wall. What is the new value for κ?
- Which would better insulate this building, a 10-cm-thick wall of brick (κ = 1.3) or a 2-cm-thick sheet of gypsum board (κ = 0.2)?
 The exterior walls of a small wooden cabin have a total cross-sectional area of 36 m2 and a thermal conductivity of 0.15 W/(m °C). Joe has discovered that he can keep the cabin 10°C warmer than the outdoors at night. To do so, however, he has to run a 500 W space heater. How thick are the cabin walls?
| |
- The Stefan–Boltzman law tells us how much energy will be emitted in the form of radiation by every square meter of an object’s surface. It reads P = εσAT4, where
- P is the emitted power in watts;
- ε is the emissivity, which ranges from 0 to 1;
- σ is a constant that equals 5.67×10−8 W m−2 K−4;
- A is the surface area in square meters; and
- T is the temperature of the surface in kelvins.
- You and your baby sister have the same body temperature and emissivity, but your surface area is four times as great as hers. What is the ratio of your thermal power to hers?
- Two space probes are in outer space, far from the Sun, but still operating thanks to their radioactive power packs. Probe A is maintaining a surface temperature of 5 K, and Probe B is at 10 K. If they are otherwise identical, what is the ratio of Probe B’s thermal power to that of Probe A?
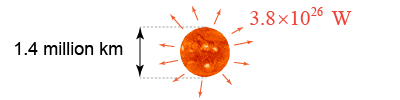
- Although it certainly isn’t black, the Sun is nearly a blackbody: Most of the light it gives off is actually thermal radiation. Use the Stefan–Boltzman law (with ε = 1) to estimate the Sun’s effective temperature in kelvins. The Sun’s diameter is 1.4 million km, and its luminosity is 3.8×1026 W.
- Once again, consider two spacecraft that are far from our Sun. They are identical except for their surface temperatures: Probe A is at 5 K and Probe B is at 10 K.
- Outer space itself has a blackbody temperature! It emits thermal radiation at a temperature of 2.7 K, chiefly in the form of microwaves. How many watts would one square meter emit if it were a perfect blackbody (ε = 1) at 2.7 K?
- The net thermal energy loss from each spacecraft takes into account the fact that the surroundings give some energy back! The formula for radiant heat transfer can be written as P = εσA(T4∞−T4), where T∞ is the temperature of the environment (outer space) and T is the temperature of the object (the probe). What is the net thermal energy transfer from each probe to outer space in watts? Each probe has an area of 4.0 m2 and an emissivity of ε = 0.5.
|
