| | Essential questions | | How are radius, velocity, acceleration, and force related in circular motion? | |
|
Many objects—from spinning wheels to the orbits of satellites around the Earth—undergo circular motion. For an object to remain in circular motion, it must experience a centripetal force (and acceleration). In this investigation, you will explore the properties of circular motion at scales similar to that of a mass swung around horizontally at the end of a string. 
|
Part 1: Directions of the velocity, force, and acceleration vectors
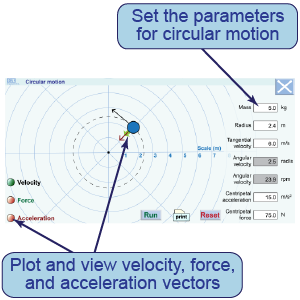
- Set m = 5.0 kg, r = 5.0 m, and v = 5.0 m/s.
- Play the simulation, and then pause it at various positions around the circle.
- Sketch the velocity, force, and acceleration vectors for at least five positions distributed around the circle.
- Which vector quantity or quantities are radial and which are tangential? Are the radial quantities pointed inward (toward the center) or outward?
- Do the lengths of the velocity, acceleration, or force vectors change around the circle?
- Notice that the angular velocity is exactly 1 rad/s. Why?

|
|
In this interactive simulation, you will investigate how velocity, acceleration, and force vary when an object is undergoing circular motion.
|
Part 2: Approximating a mass swung overhead
- Set r = 1.0 m and m = 0.3 kg.
- Calculate the tangential velocity needed to spin the object around once per second, and enter that into the simulation.
- How much force is needed to maintain this object in circular motion?
- Compare that force with the force required to hold the object motionless against the force of gravity.
- Lengthen the string to r = 2.0 m. Does it now require more or less force than before to maintain the object in circular motion with the same angular velocity?

|
Part 3: Variation of velocity with radius for circular motion
- Hold the force constant at 10 N and the mass constant at 2 kg, but vary the length of the string from r = 1 m to 5 m.
- Record the velocity and radius for each case.
- Graph v (on the vertical axis) against r and describe the shape of your graph.
- Graph v2 against r, describe the shape of your graph, and measure its slope (including units).

|
| |
|

