|
The equations of general relativity are so complex that even Einstein thought they might have no exact solutions. Later in 1915, however, German physicist Karl Schwarzschild found an exact analytical solution, which described a point mass with infinite density. Although Schwarzschild’s solution was mathematically interesting, no one took it very seriously for nearly 40 years. The term “black hole” was coined by American physicist John Wheeler in 1967 while jokingly trying to describe what Schwarzschild’s theoretical singularity might look like. Wheeler had a gift for colorful phrases and the name stuck, although virtually no one believed it was anything real. A point mass with infinite density that stopped time and sucked in mass and light like a cosmic vacuum cleaner was an absurd idea. Then, in 1972, astronomers actually found one! 
 |
Although a physicist, Schwarzschild served in the army during the First World War as an artillery officer on the Russian Front. Whenever he had free time, he experimented mathematically with Einstein’s new equations for general relativity. By expressing the system in polar coordinates, Schwarzschild found a solution that was a point mass of infinite density. He did not think the solution was real, but it was the first known exact solution to the equations. Even Einstein himself had found only an approximate solution. Schwarzschild wrote to Einstein in December 1915, “As you see, the war treated me kindly enough, in spite of the heavy gunfire, to allow me to get away from it all and take this walk in the land of your ideas.”
In 1916, Einstein wrote back, “I have read your paper with the utmost interest. I had not expected that one could formulate the exact solution of the problem in such a simple way. I liked very much your mathematical treatment of the subject. Next Thursday I shall present the work to the Academy with a few words of explanation.”
Unfortunately, Schwarzchild died the following year. The idea of a point mass of infinite density became a mathematical curiosity and was considered impossible for the next 40 years. Of course, then the astronomers started finding them! 
|
To understand a black hole, consider a rocket leaving Earth. If the rocket does not go fast enough, the Earth’s gravity eventually pulls it back to the ground. The minimum speed a rocket must go to escape the planet’s gravity is called its escape velocity. The escape velocity from Earth’s surface is approximately 11,200 m/s. Light emitted from Earth escapes easily to space because Earth’s escape velocity is far less than the speed of light (299,792,458 m/s).
|
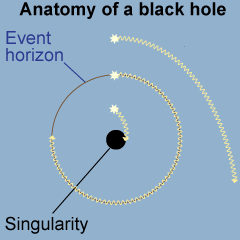A black hole is an object that is both small enough and massive enough that its escape velocity equals the speed of light. The event horizon is the radius at which the speed of light equals the orbital velocity. An object outside the event horizon may escape if it has sufficient velocity. Inside the event horizon nothing can escape. To be a black hole, a very large mass must be compressed into a very tiny space. For example, a black hole with Earth’s mass would have an event horizon the diameter of a dime.
|
|
In a sense, the region inside the event horizon is outside our universe because no matter, energy, or information can get out. At the center of the event horizon may be a singularity, Schwarzschild’s point of infinite density. No one knows what is inside, but astronomers have found many black holes in the universe. While you cannot see a black hole itself, any mass that falls into one loses so much potential energy that the area around the black hole gives off incredibly bright radiation. Astronomers believe supermassive black holes are at the core of most galaxies. Our own Milky Way contains a monster black hole with a mass of approximately four million times that of the Sun. The Galactic Center—the core of our Galaxy—is an inhospitable place for life as whole stars are consumed in a whirling maelstrom of radiation and fury. In the past two decades, astronomers have even been able to track individual stars as they orbit around the center of the Galaxy!
|
| |
|
