|
Consider our previous example. A solid rod is held at one end by a person’s hand, fixing the temperature at about 30ºC. The other end is immersed in boiling water at 100ºC. The heat flows through a length of 20 cm, or 0.2 m, between the water surface and the hand. The rod has a diameter of 1.9 cm. What is the rate of heat flow if the material is copper compared to wood? 
|
| | | P | = | power (W) | | κ | = | thermal conductivity (W m−1 °C−1) | | A | = | cross-sectional area (m2) | | L | = | length (m) | | ΔT | = | temperature difference (°C) |
| Heat conduction
|
|
When analyzing any conduction problem the first step is to identify the geometry so that you can determine the appropriate area A and length L. - Heat flows in the direction from higher temperature to lower temperature.
- The length L in equation (24.1) is measured along the direction the heat flows.
- The area A in equation (24.1) is perpendicular to the direction heat flows.
|
|
|
In this situation the two ends of the rod are at different temperatures, so heat flows along the length of the rod from the hotter end to the cooler end. The value of L is therefore measured along the rod’s length. The heat crosses through the cross-sectional area (πr2) of the rod, and therefore A = πr2.
|
|
|
Notice that 40 J of heat per second (40 W) flows up the copper rod while only 0.011 J of heat per second (0.011 W) flows up the wood rod. This is a good reason to use wood for spoon handles instead of copper! A heat flow of 40 W can raise the temperature of your skin by about 5°F per second—reaching the boiling point of water in 25 s.
|
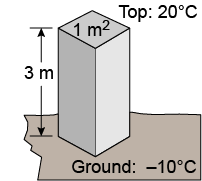A 1 m2 concrete pier that is 3 m high sits on frozen ground at a temperature of −10ºC. The top of the pier is in a room where the temperature is 20ºC. What is the rate of heat flow conducted through the pier? The thermal conductivity of concrete is about 1 W/(m ºC). - ⅓ W
- 3 W
- 10 W
- 30 W
 |
The answer is c, 10 W: 
|
