|
The superposition principle describes what happens when multiple waves overlap. It states that the wave amplitude at any place and time is the sum of the amplitudes from each individual wave. Interference is one possible result of superposition. When the combined amplitude of two waves is larger than either of the individual waves, the interference is constructive. If the combined amplitude decreases, the interference is destructive. A standing wave occurs when a wave interferes with its own reflection; it is characterized by nodes (places where the amplitude remains zero) and antinodes (where the amplitude is largest). In wave physics, resonance refers to the fact that certain physical systems will only sustain standing waves with certain frequencies. Resonance allows objects such as guitar strings and organ pipes to produce distinct musical notes. 
|
|
superposition principle, constructive interference, destructive interference, node, antinode, mode, standing wave
|
Review problems and questions |
|
- Is it possible for two waves to have individual amplitudes that are not zero while the sum of the two waves has an amplitude of zero? Explain.

 |
Yes, it is possible. This is called destructive interference and happens when the waves are 180° out of phase. Noise-canceling headphones use this physical principle to eliminate certain sounds. 
|
- Give three examples in which wave behaviors such as reflection, refraction, and absorption help doctors diagnose their patients’ medical conditions.

 |
Images taken using x-ray absorption are used to diagnose broken bones. Magnetic resonance imaging (or MRI) uses the absorption of radio-frequency waves by hydrogen atoms to highlight internal organs and tissue. MRI also depends upon the atoms’ resonance with the finely tuned radio waves. The refraction of high-frequency sound waves is used to create ultrasound images. 
|
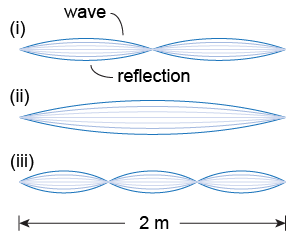
- Two friends stand on either end of a rope of length 2 m. One friend repeatedly shakes her end of the rope up and down by a few centimeters. By shaking the rope at different rates (frequencies), she generates all three of the standing-wave patterns shown here.
- In Pattern (i), what is the wavelength of the wave?
- Suppose that she completes one up-and-down hand motion in half a second (0.5 s) to generate Pattern (i). What are the period, frequency, and wave speed?
- Next, she generates Pattern (ii). What has doubled, the wavelength or the frequency?
- In Pattern (iii), how many wavelengths fit between the two ends of the rope?
- Which pattern represents the rope’s fundamental mode of vibration?

 |
Answer: - 2 m
- The period is 0.5 s, the frequency is 2 Hz, and the wave speed is 4 m/s.
- The wavelength has doubled.
- One and a half wavelengths fit within the 2-m span.
- Pattern (ii) is the fundamental mode.
Solution: - The wavelength λ of Pattern (i) is 2 m. One complete wavelength arcs both above and below the average position. In other words, if a standing wave is one wavelength long, it has three nodes and two antinodes, just like the image on page 428.
- For Pattern (i), the period is 0.5 s, the frequency is 2 Hz, and the wave speed is 4 m/s. The period is the time required for one complete up-and-down motion cycle, and that is given as half a second. The frequency (in hertz) is the reciprocal of the period (when given in seconds). The wave speed is the product of wavelength and frequency (or wavelength divided by period).
- In Pattern (i), the wavelength has doubled when compared to Pattern (i). Note that the distance between adjacent nodes is now 2 m rather than one. If we assume that wave speed remains constant (a reasonable assumption in this instance), then the frequency has been divided by a factor of 2 and the period has doubled (the student is now moving the rope up and down once per second).
- In Pattern (iii), one and a half wavelengths fit within the 2-m span. The wavelength is thus (2/3)×(2 m), or 4/3 m (approximately 133 cm).
- Pattern (ii) is the fundamental mode because it has the longest wavelength possible. That is, a wave can no longer fit, since the two ends have to be nodes for a standing wave to exist here.

|
- For each standing wave pattern shown in the figure above, how many nodes are present? How many antinodes?

 |
Pattern (i) has 3 nodes and 2 antinodes.
Pattern (ii) has 2 nodes and 1 antinode.
Pattern (iii) has 4 nodes and 3 antinodes. 
|
- For a standing wave on a stretched string, what is the relationship between the number of nodes and the number of antinodes?

 |
For standing waves on a stretched string, there is always one more node than antinode. 
|
Take a Quiz |

