|
Space is three dimensional and waves can cause oscillations in all three dimensions as well as scalar oscillations that have no direction. How a wave oscillates relative to its direction of motion is one important way to classify waves. To explain this we define the forward dimension as the direction the wave moves. The other two dimensions—up–down and left–right—are both perpendicular to the direction the wave moves. 
|
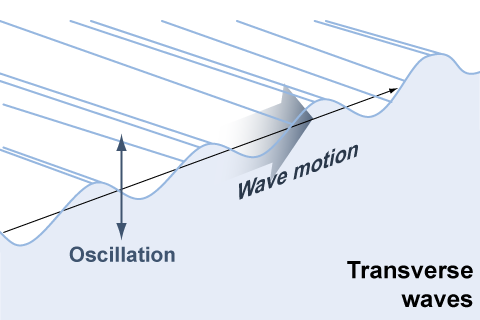A transverse wave causes oscillations perpendicular to the forward direction the wave moves. Waves in a stretched string are transverse waves because the wave moves along the string and the oscillations are up and down, perpendicular to the line of the string. Light is also a transverse wave, although the explanation for why will have to wait until Chapter 22 when we discuss electric and magnetic fields.
 |
Water waves may appear at first glance to be simple transverse waves, but in fact they are slightly different. When a transverse mechanical wave passes through a medium, the particles of that medium oscillate at right angles to the wave velocity. But when a water wave passes by, the water particles actually move both up and down and side to side. The combination of these motions is a circular path! 
|
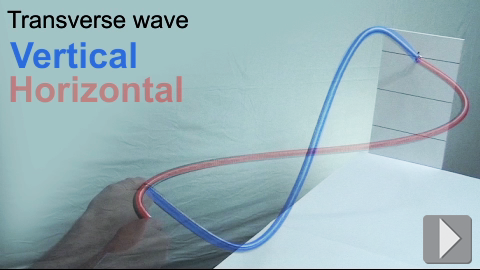A spring can be used to create transverse waves. Shaking a long spring up and down versus side to side demonstrates the property of polarization that is common to all transverse waves. Polarization describes the direction of the oscillation in a plane perpendicular to the direction the wave moves. A transverse wave has a polarization because there are two directions perpendicular to the motion of the wave. For example, a wave on a spring moving in the z-direction could be polarized in the horizontal x-direction, the vertical y-direction, or any other direction in between.
|
