 The International Astronomical Union in 2006 adopted new definitions for planets and dwarf planets:
“(1) A planet is a celestial body that (a) is in orbit around the Sun, (b) has sufficient mass for its self-gravity to overcome rigid-body forces so that it assumes a hydrostatic equilibrium (nearly round) shape, and (c) has cleared the neighborhood around its orbit.
(2) A dwarf planet is a celestial body that (a) is in orbit around the Sun, (b) has sufficient mass for its self-gravity to overcome rigid-body forces so that it assumes a hydrostatic equilibrium (nearly round) shape, (c) has not cleared the neighborhood around its orbit, and (d) is not a satellite.
(3) All other objects, except satellites, orbiting the Sun shall be referred to collectively as Small Solar System Bodies.”
- Is the Moon a dwarf planet? Why or why not?
- If the dust and rocks near a Solar System object have been swept up into its rings, is the object more likely to be a planet or a dwarf planet?
- Write one or more sentences communicating what you think is meant by “hydrostatic equilibrium” as it is written in the IAU’s text.
- Provide an example of an object that is not in hydrostatic equilibrium and communicate why you think so using one or more sentences.
- The Earth bulges out slightly along its equator. Is the Earth a planet?
- Research and write a one-page analysis of the IAU’s decision to reclassify Pluto as a dwarf planet. Cite specific data corroborating or challenging this decision.
- What is the largest diameter of circular pipe around which you can just wrap a 10 m length of string?
- If a wheel has a radius of 2 m, how far does it roll in two complete rotations?
 Robbie is swinging his favorite yo-yo in circles on a meter-long string.
- His classmate, Lucy, measures the instantaneous velocity of the yo-yo as 12 m/s. What is the centripetal acceleration of the yo-yo?
- The mass of the yo-yo is 60 g. What is the centripetal force on the yo-yo?
- David is swinging his 0.5 m long sling and exerting a centripetal force of 1,250 N. Soon he will hurl the 250 g rock in the sling at Goliath. What is the velocity of the rock as it leaves the sling?
| | 
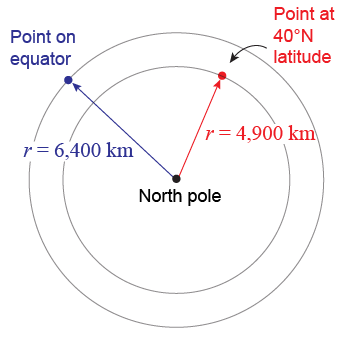
- Seen from a point above the north pole, the Earth spins (rotates) in a counterclockwise direction, and every point on its surface (other than the poles) traces a circular path around the planet’s axis. The radii of these paths are indicated here for two locations.
- With what approximate speed (in meters per second) does the equatorial spot go around the Earth’s spin axis?
- With what approximate speed (in meters per second) does the spot at 40°N latitude go around the Earth’s spin axis?
- Speculate on the reason why the USA launches most of its space probes from Florida and the Europeans launch most of theirs from the northern coast of South America.
- On a calm day, a windmill blade 4 m long turns 0.75 rad in 3 s. What is the linear velocity of the tip of the blade?
- A dragster is speeding down the track at 150 m/s. Its rear wheels are 2 m in diameter, and its front wheels are 40 cm in diameter. What are the angular velocities of the front and rear wheels, respectively?
- A 1,400 kg car traveling at 35 m/s enters a curve with a radius of 100 m.
- How much centripetal force does it take to keep the motion of a car following the curve?
- Calculate the ratio of the centripetal force from Part a to the car’s weight.
- Will the car make it around the curve? Explain.
- John is swinging a 100 g mass on a string around his head. On one end of the string is a spring scale that says he is exerting 5 N of centripetal force. Attached to the mass is a speedometer that tells him the mass is moving at 4 m/s. How long is the string?
|
