|
Problems involving centripetal acceleration often ask for the speed or radius at which the centripetal acceleration meets a specified value. For example, the safe radius for a curve on a roadway depends on the speed of the cars on that road. High-speed roads require large-radius curves. The redline for a car engine is related to the centripetal acceleration applied to the piston by the rotating crankshaft. If the engine spins too fast the force required to accelerate the piston breaks the connecting rod in a spectacular (and expensive) engine malfunction. 
|
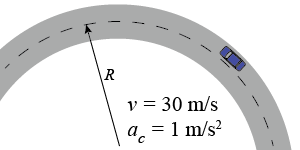The Federal Highway Association guidelines suggest a maximum safe sideways acceleration in a turn of 0.1g, or 1 m/s2. What is the minimum radius at which a civil engineer should design a curve on a road intended for cars traveling at up to 30 m/s (67 mph)?
|
| Asked: | radius R | | Given: | v = 30 m/s, ac = 1 m/s2 | | Relationships: | ac = v2/R | | Solution: | Solve the equation for the radius: ac = v2/R → R = v2/ac R = (30 m/s)2 ÷ (1 m/s2) = 900 m The minimum radius is 900 m (about 3,000 ft). |
 |
Think about the answer above: The curve for a highway must have a radius of nearly one kilometer. Many roads have sharper turns than this! The radius for highway curves can be made significantly smaller by requiring cars to drive more slowly, such as the 30 mph posted limits that are more commonly found for the on and off ramps in a cloverleaf interchange. Alternatively, the roadway surface can be banked, a design that is also used for indoor cycling tracks! 
|
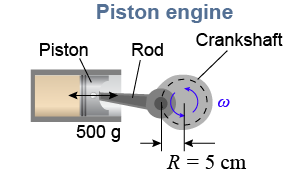A high-performance car engine has a piston and connecting rod that have a combined reciprocating mass of 500 g. The connecting rod can safely sustain a force of 20,000 N. The radius of the crankshaft is 5.0 cm (0.050 m). What is the maximum safe operating speed of the engine in revolutions per minute?
|
| Asked: | rotational speed ω in rpm | | Given: | m = 0.500 kg, F = 20,000 N, R = 0.050 m | | Relationships: | Fc = mv2/R, v = ωR, 1 rad/s = 9.55 rpm | | Solution: | First, put the force equation in terms of angular speed ω: Next, calculate ω: | | Answer: | 8,500 rpm |
|
