|
The electric field is defined by equation (18.2). Equation (18.2) says that the force F on a positive test charge q is equal to the charge multiplied by the electric field strength E at that point in space. The equation also defines the electric field E as the force F on the charged object divided by the amount of charge q. 
|
| (18.2) | | | E | = | electric field (N/C) | | Fe | = | electric force (N) | | q | = | electric charge (C) |
| Electric field
and electric force |
|
|
|
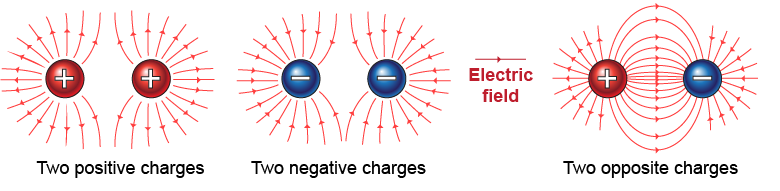
Consider the electric field around two point charges. At any position in space, the electric field E is the force on an imaginary positive test charge at that position. A positive test charge is repelled by both positive charges, so the field lines point outward from each positive charge. A positive test charge is attracted to both negative charges, so the electric field lines point toward each negative charge.
|
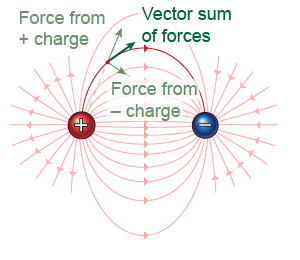The net force on a test charge at any position is the sum of the individual forces exerted by each charge in the system. The electric field between a positive and negative charge generally points away from the positive charge and toward the negative charge. Between the charges the field points directly from positive to negative. At any point in space, the total electric field is the vector sum of the field from the positive charge and the field from the negative charge as if each were independent.
 |
On a force field or electric field diagram, the density of field lines is an indication of the strength of the field. In the illustration above, the regions where the field lines are “bunched up” are the locations of the strongest electric field, such as in the region between the positive and negative charges, or close to either charge. Similarly, the field strength is low where the field lines are spaced far apart, such as in the outer regions of each illustration on this page. 
|
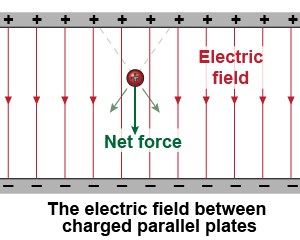What is the force on a positive test charge located between two oppositely charged parallel plates? The horizontal components of force cancel, leaving only a vertical force. Therefore, the electric field between parallel plates is purely vertical and points from the positive plate to the negative plate. The electric field is also constant in strength in the space between the plates. Why is it constant? Consider a positive test charge between the plates. When it moves away from the positive plate the repulsive force diminishes, but it simultaneously moves closer to the negative plate, causing the attractive force to increase. The two effects combine to create a constant electric field. Parallel plates are often used in experiments because they create a constant electric field and are found inside the capacitor, a commonly used device found in many electrical circuits.
|
As you will learn in the next section, the direction of the electric field curves a bit around the end of the charged parallel plates, which you can think of as an “edge effect.” If the parallel plates are infinitely long, there is no “edge” to the plates and hence no curvature for the electric field. In other words, the electric field around infinitely long, charged parallel plates is in the same direction everywhere. The electric field lines are parallel to each other.
Even a single, infinitely long, and charged plate produces electric field lines that are in the same direction everywhere and parallel to each other. Because the electric field lines are evenly spaced everywhere around a single and infinite plate, the electric field is constant everywhere around it. It doesn’t take two oppositely charged, parallel plates to create a uniform electric field—it can be done with a single, infinitely long plate, too!
|
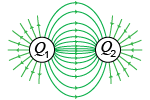In the illustration at right, what is the charge Q1? - positive
- negative
- neutral
- There is not enough information.
 |
The correct answer is a, positive. A positive test charge would be repelled from a positive object, so the field lines point away from it. 
|
