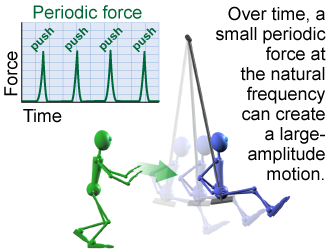|
The connection between force and motion is more complex for harmonic motion than it is for linear motion. The difference is that forces can be periodic. A periodic force is a force that repeats in cycles—like the repeated push–wait–push–wait–push—that you use to get a swing going. Of course, Newton’s laws still apply, but the frequency of a periodic force is a new variable that can make a huge difference. When the frequency of the force matches a system’s natural frequency, even a small force can produce a surprisingly large oscillation. The effect is called resonance, and it is found throughout both nature and technology. 
|
|
Think about pushing someone on a swing. A swing is a pendulum and it has a natural frequency. To create a large amplitude you supply a small push every time the swing reaches the end of its cycle. In the language of physics, your repetitive pushes are a periodic force at the natural frequency of the swing. Over many pushes, the swing builds up a large amplitude of motion even though any single push does not do much by itself.
|
|
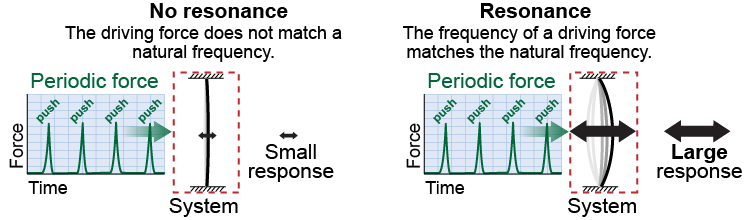
When the frequencies of the force and the system are matched, each push comes at just the right moment and the amplitude increases dramatically. This behavior is called resonance. Resonance occurs when the frequency of a periodic force matches the natural frequency of a system. Although the physical laws are the same as for linear motion, resonance is a unique behavior of harmonic motion.
|
|
|
A resonant system accumulates energy with every cycle of the applied force. A system in resonance is a very efficient energy accumulator. This is useful in technology because the energy is concentrated at the natural frequency! If you want a musical instrument to have a vibration of 100 Hz, you create something physical that has a natural frequency of 100 Hz. By doing this, only vibrations at a frequency of 100 Hz will have a large amplitude. This is the principle behind musical instruments and modern communications technologies. When you tune the FM stereo in your car what you are doing is adjusting the resonance frequency of your car’s receiver to match the frequency transmitted by a particular station.
|
In 1940, the Tacoma Narrows Bridge in Washington State vibrated and twisted amid 40 mph winds, resulting in its dramatic collapse caught on video (at left). Was this a real-world example of forced resonance, where the oscillatory frequency of the wind matched the natural frequency of the bridge? Watch the video and decide for yourself.
 |
The collapse of the Tacoma Narrows Bridge in 1940 is often used as an example of forced resonance of a mechanical oscillator, where an external force is applied at a frequency matching the natural frequency of the object. The video shows vividly how the bridge began to twist and oscillate at its natural frequency with ever-increasing amplitude until it broke apart. The frequency was measured from the video to be around 0.2 Hz, corresponding to a period of 5 s. What was the source of the periodic impulses that led to its oscillatory behavior?
The explanation often found in popular articles, websites, and even introductory physics textbooks(!) is that gusting winds provided the external frequency that drove the oscillations of the bridge deck. Wind gusts, however, are quite simply not periodic in a way that can cause forced resonance.
Another, more sophisticated explanation is sometimes offered: Periodic vortices (masses of swirling air) were generated in the wake of the bridge deck, and these vortices were spawned (or shedded) off the deck at a periodic frequency that drove the bridge oscillation. These Strouhal vortices would have trailed behind the deck and aligned in two rows (above and below) with opposite directions of circulation. The frequency of these “shedding vortices,” however, has been shown to differ substantially from the observed frequency of oscillation of the bridge prior to its collapse. Furthermore, the forces caused by Strouhal vortices leads to roller-coaster-like (but safe) vertical oscillations, not the twisting oscillations that were observed in the 45 minutes prior to collapse. Incidentally, these vertical oscillations had been observed on the bridge in low-wind-speed conditions in the preceding months, and locals had informally dubbed the bridge “Galloping Gertie.”
If not oscillating wind or Strouhal vortices, then what caused the oscillations? A recent review of a half-century’s worth of engineering literature indicated that the bridge underwent torsional (or twisting) oscillations caused by “aeroelastic fluttering.” The wind passing over the bridge generated vortices on either side of the bridge deck. When the angle of attack between the wind and the bridge deck changed—whether as a result of small twisting of the deck or a small change in the direction of the wind—the bridge deck shedded new vortices into the air in its wake. The properties of the shedded vortices in this motion-induced wake are asymmetrical and can exert forces (or torques) back on the bridge deck. The feedback from these torsional forces caused the bridge deck’s angle of attack to change again, thus leading to new torsional forces on the deck. At high wind speed these oscillatory torsional forces, induced by structural motion of the bridge itself, matched a natural frequency of the bridge and caused a runaway feedback loop. The Tacoma Narrows Bridge was destroyed by torsional oscillations caused by a flutter wake (or aeroelastic fluttering) that was, in turn, caused by the changes in the angle of attack between the bridge and the wind.
The popular explanation of the Tacoma Narrows Bridge collapse as forced resonance, where the high winds provided an external periodic frequency matching the natural frequency of the bridge, is, at best, an oversimplification of what happened. The source of the bridge’s violent oscillations were not general oscillations in the wind but were instead self-induced in the air by the bridge itself: Although the wind provided the energy input to the system, it was motion of the bridge (or changing angle of attack) that provided the mechanism to tap into that energy. Regardless of the detailed physical explanation, the dramatic video of the event is nothing short of amazing to watch!
For the decades following the bridge collapse, engineers studied the video of the incident, conducted wind tunnel experiments with a scale model, and calculated in detail how the bridge and air interacted with each other. The goal was to understand the physics behind the collapse and improve engineering designs of future bridges to prevent a similar catastrophe. The Bronx-Whitestone Bridge in New York City was built around the same time as, and with a similar design to, the Tacoma Narrows Bridge. Cable stays were subsequently attached to the towers and steel trusses mounted along the edge of the bridge deck to prevent a failure like that in Washington state. The steel trusses were replaced in 2003 with lighter fiberglass fairings that remain to this day. 
|
Which of the following is not an example of resonance? - a trumpet player vibrating his lips to make a note
- a child bouncing a ball up and down
- a singer singing a specific note for a glass to vibrate and break
- a person pushing another on a swing set
 |
The correct answer is b. Although bouncing a ball includes a periodic force and cyclic motion, the answer does not imply that this force is interacting with a system to cause resonance. 
|
| |
|
