| | Essential questions | | How do we understand motion that repeats in cycles? | |
|
A pendulum and a mass on a spring are both good examples of oscillators, or systems that exhibit repetitive behavior. This investigation looks at how motion characteristics such as period and frequency are affected by physical variables such as mass, length, and spring constant. 
|
Part 1: Period of a pendulum
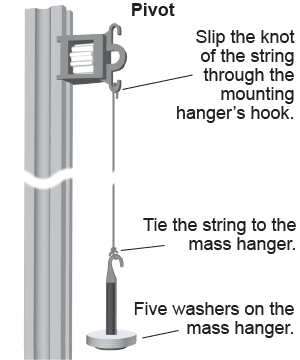
- Attach the pendulum as shown.
- Set five washers on the hanger for the mass.
- Set the pendulum swinging and observe the motion.
- With a stopwatch, measure the time to complete 10 full cycles.
- Change the amplitude, mass, and string length one at a time and see how each variable affects the period of your pendulum.
- Describe how you determined one full cycle of the pendulum.
- How does the period of the pendulum depend on length, mass, and amplitude? Support your answers using the data.
- Propose a design for a pendulum that has a period of 2.0 s.
- How did you choose the number of trials for each variable?

|
|
Use this electronic utility as a stopwatch to time the pendulum oscillations.
|
Part 2: Mass and spring oscillator
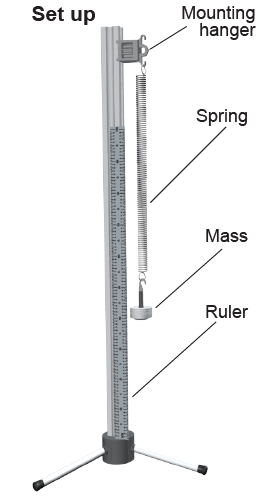
- Set 20 washers on the mass hanger. Attach the mass and spring. Place the meter rule against the stand. Note the marking on the ruler that aligns with the top washer in its equilibrium position.
- Displace the mass 5 cm and release it. Record the time to complete 10 oscillations.
- Repeat the experiment and record data for different masses and amplitudes.
- Replace the first spring with a large rubber band (or a second spring of a different length) and set 20 washers on the mass hanger.
- With a stopwatch, measure the time to complete 10 oscillations.
- With a spring scale, measure and record the force needed to extend each spring/band by 10 cm. Calculate the spring constants. The spring constant is k = F/x, where F is in newtons and x is in meters.
- How did you determine one full cycle of the motion?
- How does the period of the mass–spring oscillator depend on mass and amplitude? Your answer should be supported by the data.
- Explain the answer to part b using Newton’s second law.
- How does the period of the mass–spring oscillator depend on the spring constant? Your answer should be supported by the data.
- In step 3 above, what were the independent, dependent, and controlled variables?

|
| |
|

