|
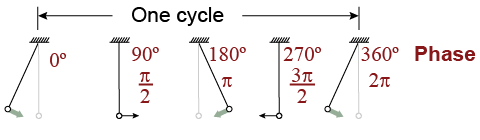
A rotating wheel returns to the same place every 360°, giving rotation a cycle, just like harmonic motion. A useful difference is that each cycle of circular motion always has a “period” of 2π rad or 360°. For this reason, the 2π (360º) cycle of circular motion is used to represent the periodicity of all forms of harmonic motion. 
| 
|
|
The fraction of a full circle is a useful idea to describe where any oscillator is within its full cycle. For example, a pendulum that is one-quarter of the way through its cycle is described as having a phase of 90º or π/2. The word phase refers to where an oscillator is at a particular moment in relation to its full cycle. If we let one cycle be 360°, then one-quarter of a cycle is 90°. In radians, a full cycle is 2π rad, and therefore a quarter-cycle is π/2 rad. 
|
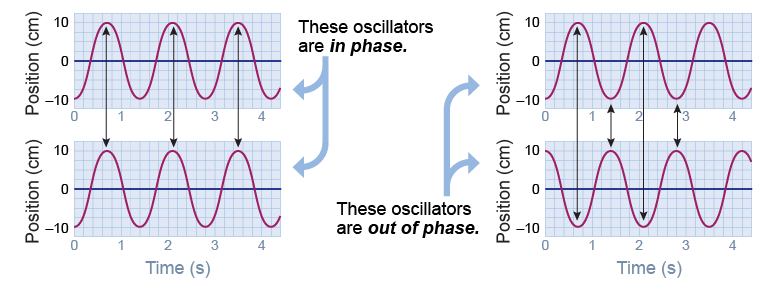
Two oscillators may have the same period but different phases. For example, if you start two identical pendulums together, their position versus time graphs would look like the diagram on the left. These pendulums are in phase because each is always at the same position at the same time. 
|
|
Consider the graphs if one pendulum is started when the other is halfway through its cycle. When the first pendulum is at its extreme left, the second is at its extreme right. The graphs of position versus time have the same cycle, but they are out of phase with each other. The second pendulum is always 180° (π) behind the first. The graph shows the lead of the first pendulum as a phase difference. These two pendulums are out of phase by 180°, or one-half cycle. Oscillators may differ in phase by any amount between 0º and 360º (0–2π rad). 
|
| |
|

