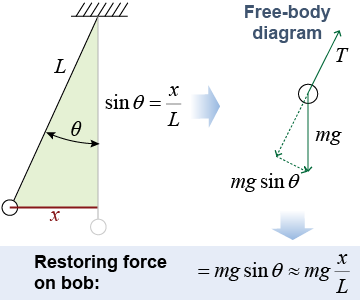Essential Physics

Natural frequency of a pendulum


How can we calculate the period of a pendulum?	Consider a pendulum displaced a distance x from center, such that the string makes an angle θ with the vertical. Upon release, it oscillates with amplitude x. The restoring force on the pendulum bob is a component of the gravitational force: $F_{r e s t o r i n g} = m g \sin θ = m g \frac{x}{L}$ From Newton’s second law we know that the acceleration a is the force divided by the mass. This tells us the maximum acceleration of the pendulum bob: $a = \frac{F}{m} \to a_{\max} = g \frac{x}{L}$
Estimating the period	The pendulum bob has zero tangential acceleration at the center, so we approximate the average acceleration a as one half the maximum, or $a = \frac{g x}{2 L}$ From the equations for accelerated motion we know that the displacement x is given by x = ½at² for an object that moves with constant acceleration a starting from rest. If we solve this for the time t we get an estimate of the time it takes the pendulum to move the distance x: $\begin{matrix} x = x_{0} + v_{0} t + \frac{1}{2} a t^{2} & \Rightarrow & t = \sqrt{\frac{2 x}{a}} & \Rightarrow & t = \sqrt{\frac{2 x}{\frac{g x}{2 L}}} \end{matrix}$
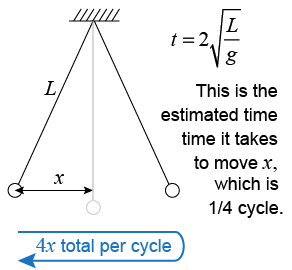What does the estimate tell us?	When we simplify the fraction under the square root, the amplitude x cancels out! To get the period of the pendulum, we multiply by four because the pendulum moves approximately 4x in one cycle. We are left with a simple formula that tells us that the period of a pendulum depends only on gravity and the square root of the length of the string!
Why doesn’t the amplitude matter?	How does it make sense that period does not depend on the amplitude? The answer is that the time it takes to travel a certain distance depends on both the distance and the speed. As the pendulum is displaced more from equilibrium it is lifted higher as well. The additional height adds energy and makes the pendulum move faster. The effect of longer distance is almost exactly compensated by the greater speed, so the time remains about the same. A careful experiment, however, will show that the period of a pendulum does depend on its amplitude! The effect is small, but it is a few percent and enough to make pendulum-driven clocks inaccurate. The falling weight of a grandfather clock and the wound mainspring of a wind-up clock are mechanisms that slowly add energy to keep the amplitude of the pendulum nearly constant.
How does this compare to an exact calculation?	$Estimate: t_{p e r i o d} \approx 8 \sqrt{\frac{L}{g}} Actual solution: t_{p e r i o d} = 2 π \sqrt{\frac{L}{g}}$ In a more advanced physics class, you may derive the period of oscillation for the simple pendulum; if so, you will find that it gives a factor of 2π instead of 8. Nonetheless, the dependence on the square root of L/g is the same. More importantly, the analysis predicts that the period of a pendulum is independent of mass and amplitude, depending only on the square root of the string length, in excellent agreement with observations.


		399