|
If you have ever used a swing you have first-hand experience of harmonic motion. A swing is physically a large pendulum, a mass suspended below a pivot point by a rope or chain, allowing the mass to oscillate back and forth. The equilibrium point is directly below the pivot, where the swing hangs at rest. The period is the time it takes to complete one full back-and-forth swing. The amplitude is the maximum distance the swing moves from its resting (center) position. 
|
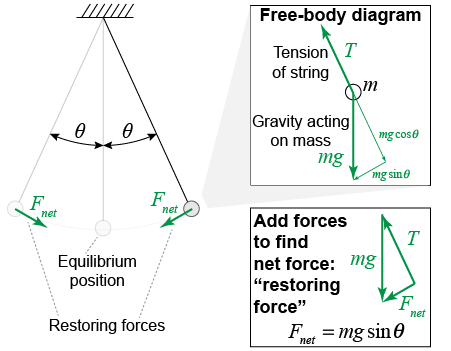The weight mg acts vertically down while the tension T acts along the string. When the string makes an angle θmax to the right, the forces along the direction of the string cancel, leaving a net force Fnet that points down and to the left—back toward equilibrium. When the string makes the same angle to the left, the net force points down and to the right. The net force pushes the bob back toward equilibrium.
 |
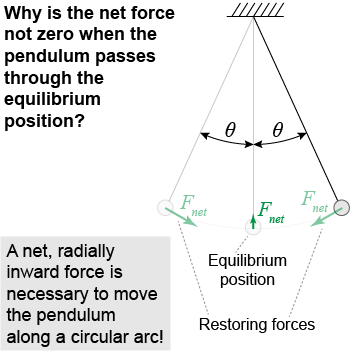If you hang the pendulum bob motionless at its equilibrium position, the net force on the bob is zero. When the pendulum is oscillating, however, the net force on the bob is not zero as it passes through the equilibrium position. Why? For the pendulum’s motion to trace out a circular arc—which is a kind of circular motion—the pendulum must experience a net force that is radially inward. An inwardly directed net force is the requirement for circular motion! The magnitude of the upward net force as it passes through equilibrium is significantly smaller than the net force the bob experiences at either extreme of its oscillatory motion. 
|
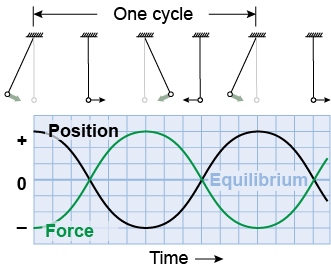As the bob moves back toward equilibrium, the restoring force goes to zero. At the center, the restoring force is zero but the pendulum keeps moving because of inertia. Past the center the force is reversed, and the bob slows, reverses direction, and moves back toward equilibrium to begin the next cycle. The pendulum crosses equilibrium twice in each cycle—once moving to the left and once to the right.
|
|
The total energy of the pendulum remains constant even though its energy changes form. At the highest point of the oscillation, it has only potential energy. As the bob moves through the equilibrium position, all of its energy has been converted into kinetic energy.
|
A pendulum is described by three variables: the mass of the bob, the length of the string, and the amplitude of the motion. Experimentally, we observe that the pendulum’s period T - depends on the square root of the string length, ,
- does not depend on its amplitude, and
- does not depend on its mass.
Why does the period depend on length but not on amplitude or mass? What is the physics behind it?
|
If a pendulum is modified so that its period increases, what can you say about the length of the pendulum? - The length was kept the same.
- The length was made shorter.
- The length was made longer.
- There is not enough information provided to answer.
 |
The answer is c, the length has been made longer. The period is proportional to the square root of the length of the pendulum. 
|
